《2025年53精准练八年级数学下册北师大版山西专版》

6. 一块麦田有$m\ km^{2}$，甲收完这块麦田需要$n\ h$，乙比甲少用$0.5\ h$就能收割完这块麦田，两人一起收割完这块麦田需要 ( )
A. $\frac{n^{2}-0.5n}{2n - 0.5}\ h$
B. $\frac{n - 0.5}{2n - 0.5}\ h$
C. $\frac{n^{2}}{2}\ h$
D. $\frac{2n - 0.5}{n^{2}-0.5n}\ h$

答案： A

7. [2024大同三模]如图所示，小敏同学不小心将分式运算的作业撕坏了一角，若已知该运算正确，则撕坏的部分中“□”代表的是________.

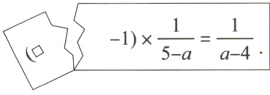
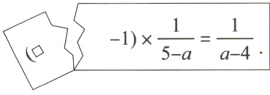
答案： $\frac{1}{a - 4}$

8. [2024嘉兴期末改编]如图，已知正方形ABCD和正方形CEFG，点E在CD边上，连接AG交CD于点H，连接BE，BH，GE.若正方形CEFG的边长为$a$，则图中阴影部分的面积为__________.

答案： $\frac{a^{2}}{2}$
详解: 如图, 延长 GF 交 AD 的延长线于点 M, 则∠M = 90°.
已知正方形 CEFG 的边长为 a, 设正方形 ABCD 的边长为 b, DH = m, 则 GM = b, DM = a, AM = a + b, DE = b - a.
∵$S_{\triangle AGM}=S_{\triangle ADH}+S_{梯形 DHGM}$,
即$\frac{1}{2}GM\cdot AM=\frac{1}{2}DH\cdot AD+\frac{1}{2}(DH + GM)\cdot DM$,
∴$\frac{1}{2}b\cdot(a + b)=\frac{1}{2}m\cdot b+\frac{1}{2}(m + b)\cdot a$,
∴$m=\frac{b^{2}}{a + b}$,
∴$EH = DH - DE=\frac{b^{2}}{a + b}-(b - a)=\frac{a^{2}}{a + b}$,
∴$S_{阴影}=S_{\triangle BEH}+S_{\triangle GEH}=\frac{1}{2}EH\cdot(BC + CG)=\frac{1}{2}\cdot\frac{a^{2}}{a + b}\cdot(b + a)=\frac{a^{2}}{2}$.

9. [2023朔州期末]先化简，再求值：$\frac{2}{a - 3}+\frac{a}{a^{2}-9}\div\frac{a^{2}-4a}{a + 3}$，其中$a$，2，4为$\triangle ABC$的三边长，且$a$为整数.

答案： 解: 原式=$\frac{2}{a - 3}+\frac{a}{(a + 3)(a - 3)}\cdot\frac{a + 3}{a(a - 4)}=\frac{2}{a - 3}+\frac{1}{(a - 3)(a - 4)}=\frac{2a - 8 + 1}{(a - 3)(a - 4)}=\frac{2a - 7}{(a - 3)(a - 4)}$.
∵ a, 2, 4 为△ABC 的三边长,
∴ 2 ＜ a ＜ 6,
∴ 整数 a 为 3, 4, 5,
∵ a - 3≠0 且 a - 4≠0,
∴ a 的值为 5.
当 a = 5 时,
原式=$\frac{2\times5 - 7}{(5 - 3)\times(5 - 4)}=\frac{3}{2}$.

10. [新定义]定义：若分式$A$与分式$B$的和等于它们的积，即$A + B = AB$，则称分式$A$与分式$B$互为“等和积分式”.如$\frac{2}{1 + x}$与$\frac{2}{1 - x}$，因为$\frac{2}{1 + x}+\frac{2}{1 - x}=\frac{4}{(1 + x)(1 - x)}=\frac{2}{1 + x}\cdot\frac{2}{1 - x}$，所以$\frac{2}{1 + x}$与$\frac{2}{1 - x}$互为“等和积分式”，其中一个分式是另外一个分式的“等和积分式”.
(1)分式$\frac{2a}{a + 1}$与分式$\frac{2a}{a - 1}$________“等和积分式”(填“互为”或“不互为”).
(2)求分式$\frac{x}{x - 3y}$的“等和积分式”.
(3)①观察(1)(2)的结果，寻找规律，直接写出分式$\frac{b}{a}$的“等和积分式”：__________；
②用发现的规律解决问题：若$\frac{m - 1}{nx + 2x}$与$\frac{n + 1}{2m - mx}$互为“等和积分式”，求实数$m$，$n$的值.

答案： 解:
(1) 互为.
详解:
∵$\frac{2a}{a + 1}+\frac{2a}{a - 1}=\frac{2a(a - 1)+2a(a + 1)}{(a + 1)(a - 1)}=\frac{4a^{2}}{(a + 1)(a - 1)}=\frac{2a}{a + 1}\cdot\frac{2a}{a - 1}$,
∴ 分式$\frac{2a}{a + 1}$与分式$\frac{2a}{a - 1}$互为 “等和积分式”.
(2) 设分式$\frac{x}{x - 3y}$的 “等和积分式” 为 A, 则$\frac{x}{x - 3y}+A=\frac{x}{x - 3y}\cdot A$,
即$\frac{x}{x - 3y}=(\frac{x}{x - 3y}-1)A$,
∴$A=\frac{x}{x - 3y}\div(\frac{x}{x - 3y}-1)=\frac{x}{x - 3y}\cdot\frac{x - 3y}{3y}=\frac{x}{3y}$,
∴ 分式$\frac{x}{x - 3y}$的 “等和积分式” 为$\frac{x}{3y}$.
(3) ①$\frac{b}{b - a}$.
② 由规律可得$\frac{m - 1}{nx + 2x}$的 “等和积分式” 为$\frac{m - 1}{m - 1 - nx - 2x}$.
∵$\frac{m - 1}{nx + 2x}$与$\frac{n + 1}{2m - mx}$互为 “等和积分式”,
∴$\begin{cases}m - 1 - nx - 2x = 2m - mx\\m - 1 = n + 1\end{cases}$,
由 m - 1 = n + 1 得 n = m - 2,
将 n = m - 2 代入 m - 1 - nx - 2x = 2m - mx, 得 m - 1-(m - 2)x - 2x = 2m - mx,
∴ m = -1.
当 m = -1 时, n = -1 - 2 = -3.
因此 m = -1, n = -3.