《2025年新课程新教材导航学七年级数学上册北师大版》

5. 第一行的平面图形绕虚线旋转一周能得到第二行的一个几何体，请用线连接起来。

答案：
5.如图.
　　

6. “枪挑一条线，棍扫一大片。”从数学的角度解释为(A)

A.点动成线，线动成面
B.线动成面，面动成体
C.点动成线，面动成体
D.点动成面，面动成线

答案： 6.A

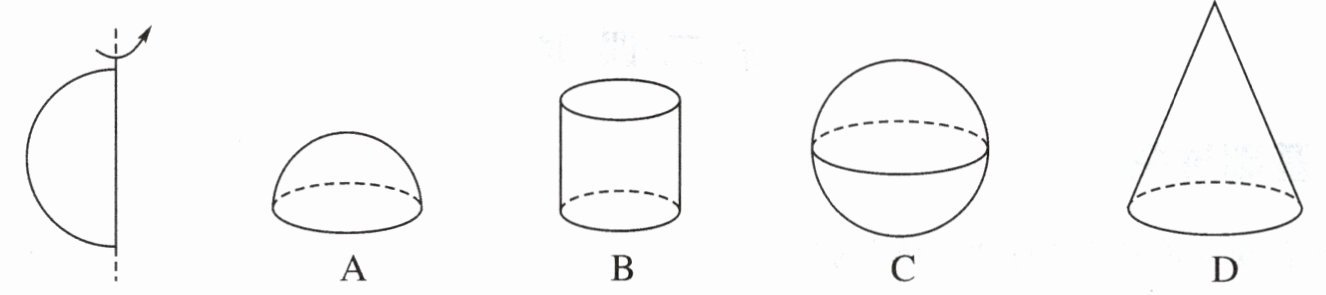
7. 如图，将平面图形绕轴旋转一周，得到的几何体是(C)

答案： 7.C

8. 纸翻花是我国传统的纸制工艺品，它花里有花，花中变花，花姿优美，栩栩如生，深受儿童的喜爱。转动翻花的花柄平面图形可变换成不同的美丽的立体图形，这说明了面动成体。

答案： 8.面动成体

9. 已知长为 $ 6 \, cm $，宽为 $ 4 \, cm $ 的长方形是一个圆柱的侧面展开图，则圆柱的体积为$\frac{24}{\pi} cm^3$ 或 $\frac{36}{\pi} cm^3$(结果保留 $ \pi $)。

答案： 9.$\frac{24}{\pi} cm^3$ 或 $\frac{36}{\pi} cm^3$

10. 现有一个长为 $ 6 \, cm $，宽为 $ 3 \, cm $ 的长方形，以它的一边所在直线为轴旋转一周，得到的几何体的体积是多少？

答案： 10.解:长方形绕着它的一边所在的直线旋转一周，得到的立体图形是圆柱.
　以6cm的边所在直线为轴旋转一周所得到的是底面半径为3cm，高为6cm的圆柱，因此体积为 $\pi×3^2×6=54\pi(cm^3)$.
　以3cm的边所在直线为轴旋转一周所得到的是底面半径为6cm，高为3cm的圆柱，因此体积为 $\pi×6^2×3=108\pi(cm^3)$.
答:得到的几何体的体积是 $54\pi cm^3$ 或 $108\pi cm^3$.