《2025年新课程新教材导航学七年级数学上册北师大版》

10. 用一根长为 80 cm 的铁丝围成一个长方形。
（1）若该长方形的长比宽多 10 cm，那么这个长方形的面积为多少平方厘米？
（2）若该长方形的长比宽多 4 cm，那么这个长方形的面积为多少平方厘米？
（3）通过比较（1）与（2）中长方形的面积的大小，写出你得出的结论。

答案： 10.解：
(1)设长方形的宽为$x cm$，则长为$(x + 10) cm$。
由题意，得$2(x + 10 + x) = 80$，解得$x = 15$。
所以$x + 10 = 25$。
则长方形的面积为$25 × 15 = 375(cm^2)$。
(2)设长方形的宽为$x cm$，则长为$(x + 4) cm$。
由题意，得$2(x + 4 + x) = 80$，解得$x = 18$。
所以$x + 4 = 22$。
则长方形的面积为$22 × 18 = 396(cm^2)$。
(3)因为$375 ＜ 396$，
所以当长方形的长和宽越接近时，面积越大。(答案不唯一，合理即可)

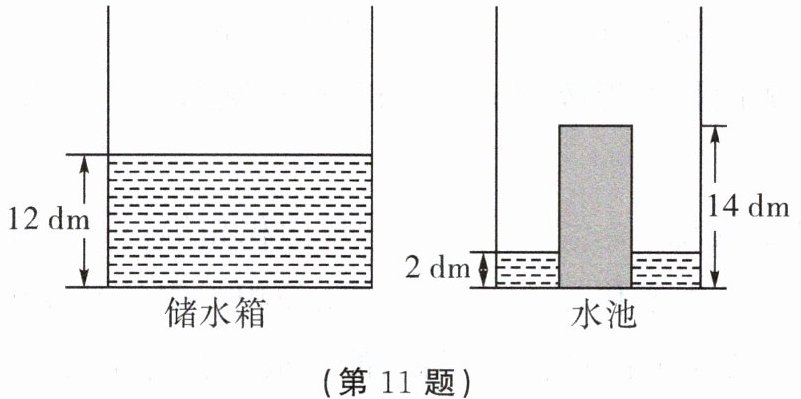
11. 如图是一个长方体储水箱和一个长方体水池的侧面示意图(厚度忽略不计)，储水箱中水深 12 dm，把一高度为 14 dm 的长方体石柱放置于水池中央后，水池中水深 2 dm。现将储水箱中的水匀速注入水池，注水 4 min 时水池水面与石柱上底面持平；继续注水 2 min 后，储水箱中的水全部注入水池，此时水池中水深 19 dm。根据上述信息，解答下列问题：
(1)注水 1 min 后储水箱中的水深为10 dm。
(2)注水多长时间时，储水箱和水池中的水的深度相同？
(3)若石柱的体积为 168 $ dm^3 $，请直接写出注水前储水箱中水的体积：1080 dm^3。

答案： 11.
(1)10
(2)解：储水箱水面下降的速度为$12 ÷ (4 + 2) = 2(dm/min)$，
水池水面在前$4 min$内上升的速度为$(14 - 2) ÷ 4 = 3(dm/min)$。
设$t min$时储水箱和水池中的水的深度相同，
则$12 - 2t = 2 + 3t$，
解得$t = 2$。
答：注水$2 min$时，储水箱和水池中的水的深度相同。
(3)$1080 dm^3$