《2025年新课程新教材导航学七年级数学上册北师大版》

2. 观察下列等式，解答后面的问题：
第1个等式：$3^{2}-0× 6=9$；
第2个等式：$4^{2}-1× 7=9$；
第3个等式：$5^{2}-2× 8=9$；
第4个等式：$6^{2}-3× 9=9$；
……
（1）请直接写出第5个等式为。7^{2}-4×10=9
（2）根据上述规律猜想第$n$个等式为（用含$n$的等式表示）。(n+2)^{2}-(n-1)(n+5)=9

答案： $2.(1)7^{2}-4×10=9$
$(2)(n+2)^{2}-(n-1)(n+5)=9$

3. 小明观看了纸牌魔术表演，非常感兴趣，并做了如下实验和探究：
将几张纸牌摞起来（从上面分别记为第1张，第2张，第3张……），先将第1张牌放到整摞牌的下面，再去掉第2张牌；继续将第3张牌放在整摞牌的下面，再去掉第4张牌……如此循环往复，最终到只留下1张纸牌为止。
例如，若将4张纸牌摞起来，按上述规则操作，陆续去掉第2张、第4张、第3张，最终留下第1张纸牌。将8张纸牌摞起来，按上述规则操作，最终留下的是第张纸牌；将$m$张纸牌摞起来，按上述规则操作，若最终留下的是第1张纸牌，则$m=$（用含$n$的代数式表示，其中$n$为自然数）。12^{n}

答案： $3.1 2^{n}$

4. 乐乐设计了一个有趣的运算程序：任意写出一个三位数（各数位上的数字相同的除外），重新排列各位数字，使其组成一个最大的数和一个最小的数，然后用最大的数减去最小的数，得到差，然后把差重复这个过程。以579开始，按照此程序运算2025次后得到的数是。495

答案： 4.495

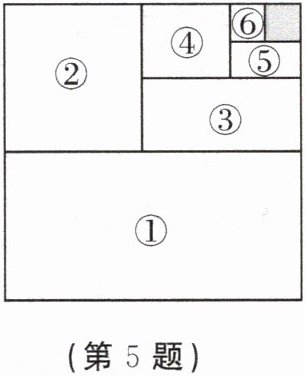
5. 如图，将一张边长为1的正方形纸片分割成7个部分，部分①是边长为1的正方形纸片面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依次类推，可求得阴影部分的面积是$\frac{1}{2^{6}}$。受此启发，$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+·s+\frac{1}{2^{6}}$的值为。类比探究：$\frac{1}{3}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+·s+\frac{1}{3^{n}}$的值为。$\frac{63}{64}$$\frac{3^{n}-1}{2 × 3^{n}}$

答案： 5.$\frac{63}{64}$ $\frac{3^{n}-1}{2 × 3^{n}}$

6. 用“字母表示数”被后人称为从“算术”到“代数”的一次飞跃。用字母表示数可以分析从特殊到一般的数学规律。请观察下列关于正整数的平方拆分的等式：
第1个等式：$2^{2}=1+1^{2}+2$；第2个等式：$3^{2}=2+2^{2}+3$；
第3个等式：$4^{2}=3+3^{2}+4$；第4个等式：$5^{2}=4+4^{2}+5$。
（1）请用此方法拆分$2025^{2}$。
（2）请你用上面的方法归纳一般结论，用含$n$（$n$为正整数）的等式表示，并借助运算证明这个结论。
（3）小林尝试借助图形的面积验证（2）中的结论，思路是将边长为$n$的正方形（如图）进行适当分割。请你帮助他完成画图，并在图中标出相应线段的长度。

答案：
6.解$:(1)2025^{2}=2024+2024^{2}+2025.$
(2)含n的等式是$n^{2}=(n-1)+(n-1)^{2}+n.$
证明:因为右边$=n-1+n^{2}-2n+1+n=n^{2},$左边$=n^{2},$所以左边=右边，
所以$n^{2}=(n-1)+(n-1)^{2}+n$成立.
(3)如图.