第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. (2025·西畴县模拟)已知一个圆锥的高为4cm,母线长为5cm,则圆锥的侧面积为(
A.$20\pi cm^{2}$
B.$12\pi cm^{2}$
C.$25\pi cm^{2}$
D.$15\pi cm^{2}$
D
)A.$20\pi cm^{2}$
B.$12\pi cm^{2}$
C.$25\pi cm^{2}$
D.$15\pi cm^{2}$
答案:
1. D
2. (2025·梅州二模)一个扇形半径3cm,圆心角120°,用它围成一个圆锥,则这个圆锥的底面周长为(
A.$\frac{1}{2}\pi cm$
B.$\pi cm$
C.$2\pi cm$
D.$3\pi cm$
C
)A.$\frac{1}{2}\pi cm$
B.$\pi cm$
C.$2\pi cm$
D.$3\pi cm$
答案:
2. C
3. 小刚用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是(

A.$120\pi cm^{2}$
B.$240\pi cm^{2}$
C.$260\pi cm^{2}$
D.$480\pi cm^{2}$
B
)
A.$120\pi cm^{2}$
B.$240\pi cm^{2}$
C.$260\pi cm^{2}$
D.$480\pi cm^{2}$
答案:
3. B
4. 如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = 3$,$BC = 5$,若把$Rt\triangle ABC$绕直线$AC$旋转一周,则所得圆锥的侧面积等于(
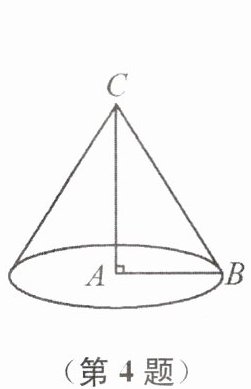
A.$6\pi$
B.$9\pi$
C.$12\pi$
D.$15\pi$
D
)
A.$6\pi$
B.$9\pi$
C.$12\pi$
D.$15\pi$
答案:
4. D
5. 如图所示,矩形纸片$ABCD$中,$AD = 6cm$,把它分割成正方形纸片$ABFE$和矩形纸片$EFCD$后,分别裁出扇形$ABF$和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则$AB$的长为(

A.3.5cm
B.4cm
C.4.5cm
D.5cm
B
)
A.3.5cm
B.4cm
C.4.5cm
D.5cm
答案:
5. B
6. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是
$24\pi$
。
答案:
$6. 24\pi$
7. (2025·牡丹江模拟)若一个圆锥的侧面积是底面积的3倍,则这个圆锥侧面展开图的圆心角等于
$120^{\circ}$
。
答案:
$7. 120^{\circ}$
8. (2023·东营)如果圆锥侧面展开图的面积是$15\pi$,母线长是5,则这个圆锥的底面半径是
3
。
答案:
8. 3
9. (2025·顺庆区二模)如图,在扇形纸片$OAB$中,$\angle O = 60^{\circ}$,$OA = 6cm$,把它沿虚线分割成一个扇形$OCD$和扇环,在扇环上裁出半径最大的圆,恰好能与扇形$OCD$与圆围成一个圆锥,则$OC$的长为
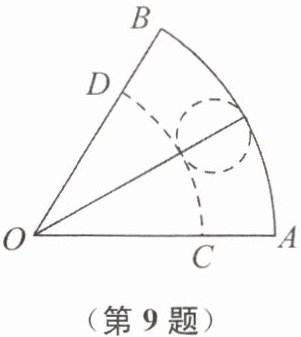
4.5
cm。
答案:
9. 4.5
查看更多完整答案,请扫码查看


