《2025年时代新课程九年级数学上册苏科版》

10. 小明家的房前有一块矩形的空地，空地上有三棵树 A，B，C，小明想建一个圆形花坛，使三棵树都在花坛的边上.
（1）在图中画出符合条件的圆(保留作图痕迹)；
（2）若$△ABC$中$AB = 8$米，$AC = 6$米，$∠BAC = 90°$，试求小明家圆形花坛的面积.

答案：
10.
(1)如图所示

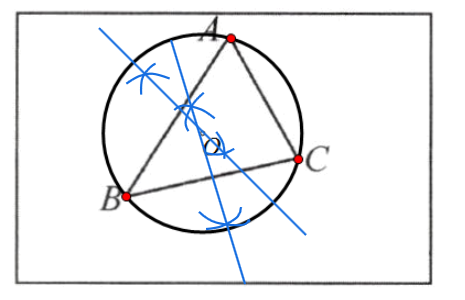
(2)$25\pi$平方米

11. 定义：到一个三角形三个顶点的距离相等的点叫做该三角形的外心.
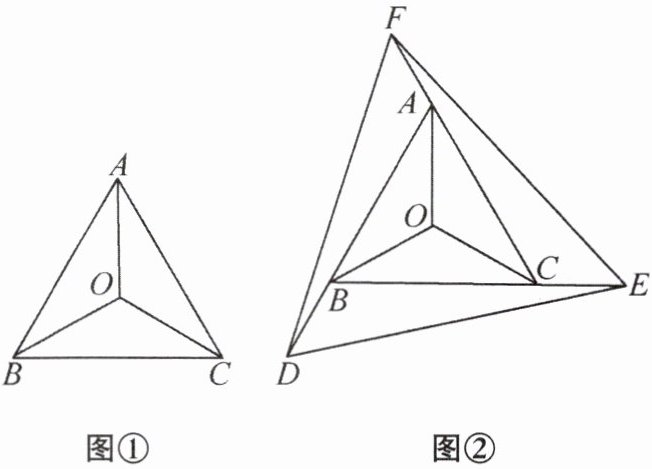
（1）如图①，$△ABC$是等边三角形，点 O 是$△ABC$的外心，求证：$∠ABO = 30°$
（2）如图②，$△ABC$是等边三角形，分别延长等边三角形 ABC 的边 AB、BC、CA 到点 D、E、F，使$BD = CE = AF$，连接 DE，EF，DF. 若点 O 为$△ABC$的外心，求证：点 O 也是$△DEF$的外心.

答案： 11.
(1)$\because \triangle ABC$是等边三角形，
$\therefore \angle ABC = 60°, AB = AC = BC$，
$\because$点$O$是$\triangle ABC$的外心，
$\therefore OA = OB = OC$，
$\therefore \triangle AOB \cong \triangle COB(SSS)$，
$\therefore \angle ABO = \angle OBC$，
$\because \angle ABO + \angle OBC = \angle ABC = 60°$，
$\therefore \angle ABO = 30°$；
(2)连接$OF, OD, OE$，
由
(1)得，$\angle ABO = 30°$，
$\because$点$O$为$\triangle ABC$的外心，
$\therefore OA = OB$，
$\therefore \angle OAB = \angle ABO = 30°$，
$\therefore \angle OAC = 30°$，
$\therefore 180° - \angle OAC = 180° - \angle ABO$，
$\therefore \angle FAO = \angle DBO$，
$\therefore \triangle FAD \cong \triangle DBO(SAS)$，
$\therefore OF = OD$，同理，$OF = OE$，
$\therefore OF = OE = OD$，
$\therefore$点$O$也是$\triangle DEF$的外心.

12. 如图，线段$AB = 6$，C 为线段 AB 上的一个动点，以 AC、BC 为边作等边$△ACD$和等边$△BCE$连接 DE，$⊙O$外接于$△CDE$，则$⊙O$半径的最小值为$\sqrt{3}$.

答案： 12.$\sqrt{3}$

13. 已知，如图 1，$△ABC$中，$BA = BC$，D 是平面内不与 A、B、C 重合的任意一点，$∠ABC = ∠DBE$，$BD = BE$.
（1）求证：$△ABD≌△CBE$；
（2）如图 2，当点 D 是$△ABC$的外接圆圆心时，请判断四边形 BDCE 的形状，并证明你的结论.

答案： 13.
(1)证明略
(2)解：四边形$BDCE$是菱形.证明如下：
同
(1)可证$\triangle ABD \cong \triangle CBE$，
$\therefore CE = AD$，
$\because$点$D$是$\triangle ABC$外接圆圆心，
$\therefore DA = DB = DC$，
又$\because BD = BE$，
$\therefore BD = BE = CE = CD$，
$\because$四边形$BDCE$是菱形.