《2025年时代新课程九年级数学上册苏科版》

10. 用尺规等分圆的方法,作正六边形、正三角形.

答案：
10.
　

11. 图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形—正八边形.
如图②,AE 是⊙O 的直径,用直尺和圆规作⊙O 的内接正八边形 ABCDEFGH(不写作法,保留作图痕迹);

答案：
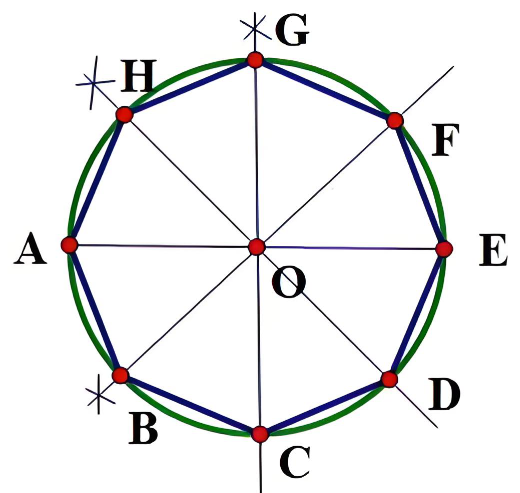
11. 如图所示

12. (2025·海港区一模)如图,正六边形 ABCDEF 的边长为 $(\sqrt{3} + 1)$,点 M 是 $\triangle ABC$ 的内心,点 N 是 $\triangle ACD$ 的外心,则 MN 的长度为(A)

A.2
B.$\sqrt{3} - 1$
C.$2\sqrt{3} - 1$
D.$2\sqrt{3} - 2$
]

答案： 12. A

13. (1)已知,如图 1, $\triangle ABC$ 是⊙O 的内接正三角形,点 P 为弧 BC 上一动点,请探究 PA,PB,PC 三者之间有何数量关系,并给予证明.
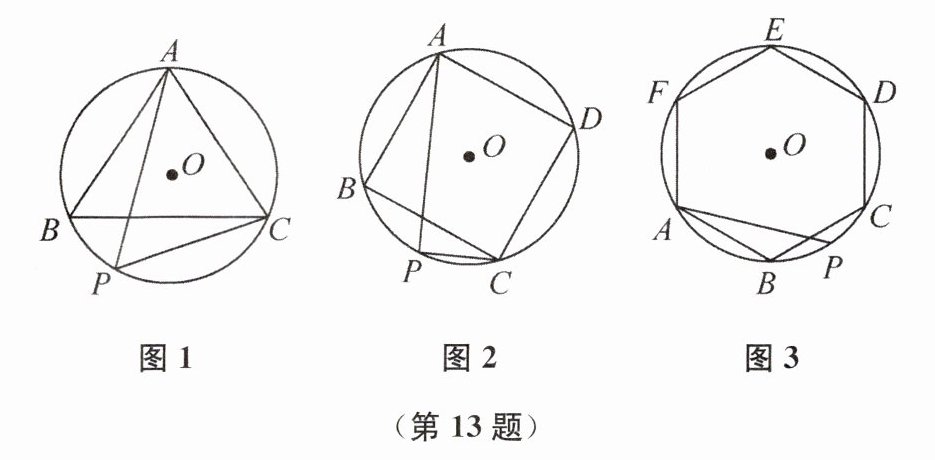
(2)如图 2,四边形 ABCD 是⊙O 的内接正方形,点 P 为弧 BC 上一动点,请探究 PA,PB,PC 三者之间有何数量关系,并给予证明.
(3)如图 3,六边形 ABCDEF 是⊙O 的内接正六边形,点 P 为弧 BC 上一动点,请探究 PA、PB、PC 三者之间有何数量关系,直接写出结论不需证明.
]

答案：
13.
(1) 提示：延长 BP 至 E，使 PE=PC，连接 CE，证明△BEC≌△APC，
∴PA=BE=PB+PC；
(2) 过点 B 作 BE⊥PB 交 PA 于 E，如图，
　　　　　　
∵∠1+∠2=∠2+∠3=90°，
∴∠1=∠3,
∴∠APB=45°，
∴BP=BE,
∴PE=$\sqrt{2}$PB，
在△ABE 和△CBP 中，$\begin{cases} BE=BP, \\ ∠1=∠3, \\ AB=BC \end{cases}$
∴△ABE≌△CBP，
∴PC=AE，
∴PA=AE+PE=PC+$\sqrt{2}$PB；
(3) PA=PC+$\sqrt{3}$PB。