《2025年时代新课程九年级数学上册苏科版》

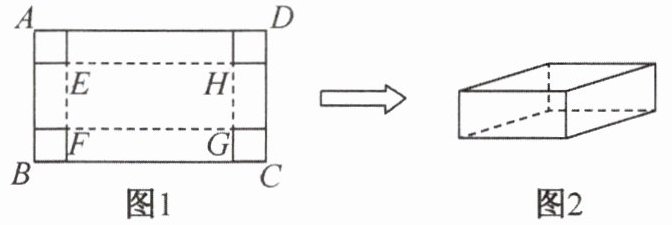
13. 在一张足够大的纸板上截取一个面积为 $ 3600 $ 平方厘米的矩形纸板 $ ABCD $,如图 $ 1 $,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形 $ EFGH $,如图 $ 2 $,设小正方形的边长为 $ x $ 厘米.
(1) 当矩形纸板 $ ABCD $ 的一边长为 $ 90 $ 厘米时,且纸盒的侧面积为 $ 1100 $ 平方厘米时,求 $ x $ 的值;
(2) 当 $ EH:EF = 7:2 $,且侧面积与底面积之比为 $ 9:7 $ 时,求 $ x $ 的值.

答案： 13.解:
(1)3600÷90=40(厘米),S侧=2[x(90−2x)+x(40−2x)]=−8x²+260x,
由题意得−8x²+260x=1100,
解得x₁=5,x₂=27.5(舍去).
(2)设EF=2m厘米,则EH=7m厘米,
则侧面积为2(7mx+2mx)=18mx,
底面积为7m·2m=14m²,
由题意,得18mx:14m²=9:7,
∴m=x,则AD=7x+2x=9x,AB=2x+2x=4x,由4x·9x=3600,且x＞0,得x=10.

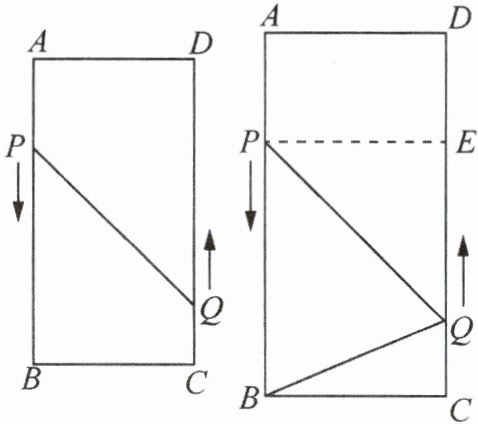
14. (2024·江阴市校级模拟)如图,在矩形 $ ABCD $ 中,$ AB = 16 \, cm, BC = 6 \, cm $,动点 $ P, Q $ 分别以 $ 3 \, cm/s, 2 \, cm/s $ 的速度从点 $ A, C $ 同时出发,沿规定路线移动.
(1) 若点 $ P $ 从点 $ A $ 移动到点 $ B $ 停止,点 $ Q $ 随点 $ P $ 的停止而停止移动,问经过多长时间 $ P, Q $ 两点之间的距离是 $ 10 \, cm $?
(2) 若点 $ P $ 沿着 $ AB \to BC \to CD $ 移动,点 $ Q $ 从点 $ C $ 移动到点 $ D $ 停止时,点 $ P $ 随点 $ Q $ 的停止而停止移动,试探求经过多长时间 $ \triangle PBQ $ 的面积为 $ 12 \, cm^2 $?

答案： 14.
(1)过点P作PE⊥CD于E,
设x秒后,点P和点Q的距离是10cm.
(16−2x−3x)²+6²=10²,
∴x₁=8/5,x₂=24/5;
∴经过8/5s或24/5s,P、Q两点之间的距离是10cm;
(2)连接BQ.设经过ys后△PBQ的面积为12cm².
①当0≤y≤16/3时,PB=16−3y,
∴1/2PB·BC=12,即1/2×(16−3y)×6=12,
解得y=4;
②当16/3≤y≤22/3时,BP=3y−16,QC=2y,
则1/2BP·CQ=1/2(3y−16)×2y=12,
解得y₁=6,y₂=−2/3(舍去);
③22/3＜y≤8时,QP=CQ−PC=22−y,
则1/2QP·CB=1/2(22−y)×6=12,
解得y=18(舍去).
综上所述,经过4秒或6秒,△PBQ的面积为12cm².