《2025年时代新课程九年级数学上册苏科版》

1. 如图所示，在 $ Rt \triangle ABC $ 中，$ \angle C = 90^{\circ} $，$ AC = 11 cm $，点 $ P $ 从点 $ A $ 出发沿 $ AC $ 以 $ 1 cm/s $ 的速度移动，点 $ Q $ 从点 $ C $ 出发沿 $ CB $ 以 $ 2 cm/s $ 的速度移动，如果 $ P $，$ Q $ 分别从 $ A $，$ C $ 两点同时出发，当它们相距 $ 10 cm $ 时所需的时间为(D)

A.$ 3 s $
B.$ 3 s $ 或 $ 1.5 s $
C.$ 5 s $
D.$ 3 s $ 或 $ 1.4 s $

答案： 1.D

2. 如图，在等腰 $ \triangle ABC $ 中，$ \angle B = 90^{\circ} $，$ AB = BC = 8 cm $，动点 $ P $ 从点 $ A $ 出发沿 $ AB $ 向点 $ B $ 移动，作 $ PQ // AC $，$ PR // BC $，当 $ □ PQCR $ 的面积为 $ \triangle ABC $ 面积的一半时，点 $ P $ 移动的路程为4 $ cm $。

答案： 2.4

3. (2025·河东区二模)如图，在 $ \triangle ABC $ 中，$ \angle B = 90^{\circ} $，$ AB = 12 mm $，$ BC = 24 mm $，动点 $ P $ 从点 $ A $ 开始沿边 $ AB $ 向点 $ B $ 以 $ 2 mm/s $ 的速度移动，动点 $ Q $ 从点 $ B $ 开始沿边 $ BC $ 向点 $ C $ 以 $ 4 mm/s $ 的速度移动，如果 $ P $，$ Q $ 两点分别从 $ A $，$ B $ 两点同时出发，设出发时间为 $ t s $。有下列结论：①当 $ t = 2 s $ 时，$ PQ = 8\sqrt{2} mm $；② $ \triangle PBQ $ 的面积可以为 $ 35 mm^2 $；③ $ t = 1 s $ 时的四边形 $ APQC $ 的面积大于 $ t = 5 s $ 时的四边形 $ APQC $ 的面积。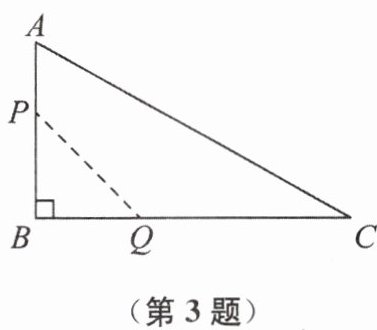其中，正确结论的是①②(填写序号)。

答案： 3.①②

4. (2023 秋·阿荣旗期末)如图所示，$ A $、$ B $、$ C $、$ D $ 是矩形的四个顶点，$ AB = 16 cm $，$ AD = 6 cm $，动点 $ P $，$ Q $ 分别从点 $ A $，$ C $ 同时出发，点 $ P $ 以 $ 3 cm/s $ 的速度向点 $ B $ 移动，一直到达点 $ B $ 为止，点 $ Q $ 以 $ 2 cm/s $ 的速度向点 $ D $ 移动
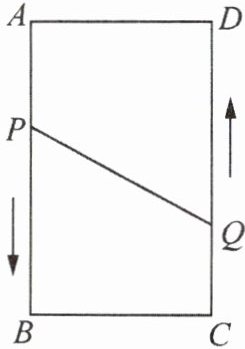
(1) $ P $，$ Q $ 两点从出发开始到几秒时，四边形 $ PBCQ $ 的面积为 $ 33 cm^2 $？
(2) $ P $，$ Q $ 两点从出发开始到几秒时，点 $ P $ 和点 $ Q $ 的距离第一次是 $ 10 cm $？

答案： 4.解：当运动时间为t秒时，PB=(16 - 3t)cm，
CQ = 2t cm.
(1)依题意，得：\frac{1}{2} × (16 - 3t + 2t) × 6 = 33，
解得：t = 5.
答：P，Q两点从出发开始到5秒时，四边形PBCQ的面积为33 $cm^{2}$.
(2)过点Q作QM⊥AB于点M，
∵PM = PB - CQ = |16 - 5t|cm，QM = 6 cm，
∴PQ^{2} = PM^{2} + QM^{2}，即10^{2} = (16 - 5t)^{2} + 6^{2}，
解得：t_{1} = \frac{8}{5}，t_{2} = \frac{24}{5}（不合题意，舍去）.
答：出发\frac{8}{5}秒时，点P和点Q的距离第一次是10 cm.