《2025年时代新课程九年级数学上册苏科版》

13. (2024 秋·沭阳县期末)已知⊙O 的半径是方程 x² - 5x - 24 = 0 的根，且点 A 到圆心 O 的距离为 6，则点 A 在(B)

A.⊙O 上
B.⊙O 内
C.⊙O 外
D.无法确定

答案： 13.B

14. (2025·盐城一模)在 Rt△ABC 中，∠C = 90°，BC = 3，AC = 4，D 为 AB 的中点。以 A 为圆心，r 为半径作⊙A，若 B、C、D 三点中只有一点在⊙A 内，则⊙A 的半径 r 的取值范围是2.5 ＜ r ≤ 4。

答案： 14.2.5 ＜ r ≤ 4

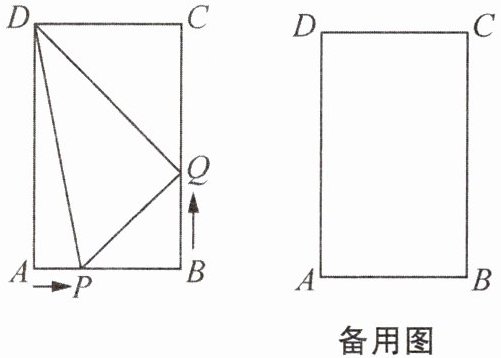
15. 如图，在矩形 ABCD 中，AB = 6 cm，BC = 12 cm，点 P 从点 A 出发沿 AB 以 1 cm/s 的速度向点 B 移动；同时，点 Q 从点 B 出发沿 BC 以 2 cm/s 的速度向点 C 移动，设运动时间为 t 秒。
(1)当 t = 2 时，△DPQ 的面积为28 cm²；
(2)运动过程中，当 A、P、Q、D 四点恰好在同一个圆上时，求 t 的值。

答案： 15.解：
(1)28;
(2)
∵∠A = 90°,
∴A、P、D三点在以DP为直径的圆上,
若点Q也在圆上,则∠PQD = 90°,
∴$PQ^{2}+DQ^{2}=DP^{2},$
∴$(6 - t)^{2}+(2t)^{2}+6^{2}+(12 - 2t)^{2}=t^{2}+12^{2};$
解得$t_{1}=6,t_{2}=\frac{3}{2},$
∴当t = 6或$\frac{3}{2}$时A、P、Q、D四点恰好在同一个圆上.

16. 阅读下列材料：
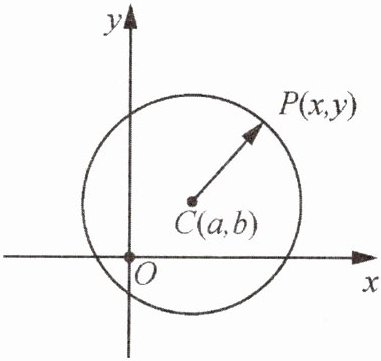
平面上两点 P₁(x₁，y₁)，P₂(x₂，y₂)之间的距离表示为 |P₁P₂| = √((x₁ - x₂)² + (y₁ - y₂)²)，称为平面内两点间的距离公式，根据该公式，如图，设 P(x，y)是圆心坐标为 C(a，b)，半径为 r 的圆上任意一点，则点 P 适合的条件可表示为 √((x - a)² + (y - b)²) = r，变形可得：(x - a)² + (y - b)² = r²，我们称其为圆心为 C(a，b)，半径为 r 的圆的标准方程。
例如：由圆的标准方程 (x - 1)² + (y - 2)² = 25 可得它的圆心为(1，2)，半径为 5。根据上述材料，结合你所学的知识，完成下列各题：
(1)圆心为 C(3，4)，半径为 2 的圆的标准方程为(x - 3)² + (y - 4)² = 4；
(2)若已知⊙C 的标准方程为 (x - 2)² + y² = 2²，圆心为 C，请判断点 A(3，-1)与⊙C 的位置关系。

答案： 16.解：$(1)(x - 3)^{2}+(y - 4)^{2}=4$
(2)由题意知圆心为C(2,0),半径为2,
∵A(3,-1),
∴$AC = \sqrt{(3 - 2)^{2}+1^{2}}=\sqrt{2}＜2,$
∴点A在⊙C内部.