《2025年时代新课程九年级数学上册苏科版》

10. (2025·海州区一模)某超市以每袋 $ 8 $ 元的成本价购进一些糖果,根据前期销售情况,每天销售量 $ y $ (袋)与该商品定价每袋 $ x $ (元)是一次函数关系,如图所示.
(1) 求销售量 $ y $ 与定价 $ x $ 之间的函数关系式;
(2) 超市准备每天销售该糖果的利润是 $ 56 $ 元,但让顾客少花钱,不考虑其它因素,求该糖果的定价应为多少.

答案： 10.
(1)y=−2x+38;
(2)由题意得:(x−8)(−2x+38)=56,
整理得:x²−27x+180=0,
解得:x₁=12,x₂=15(不符合题意,舍去),
答:该糖果的定价应为12元.

11. 大众电影院为吸引学生观看电影,推出如下的收费标准:

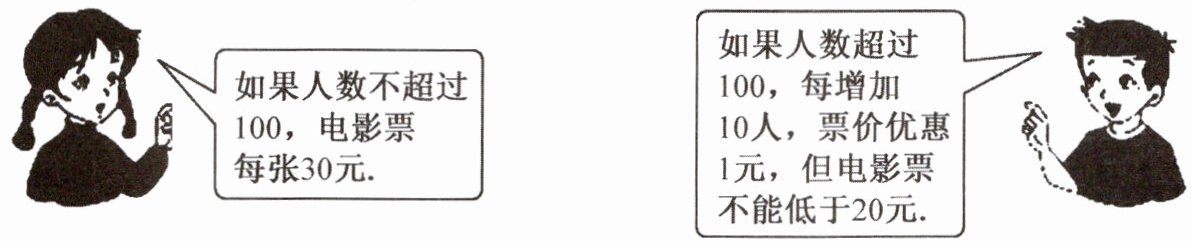
某中学组织初三学生观看电影,共支付给电影院 $ 3750 $ 元,请问共组织了多少人观看电影?

答案： 11.解:
(1)若人数不超过100,则人数为3750÷30=125,与题意不符.
(2)若人数超过100,设人数为x,
得到方程x(30−(x−100)/10)=3750,
解得x₁=150,x₂=250.
当x=150时,团体票价为25元;当x=250时,团体票价为15元,与题意不符.
经检验,x=150符合题意.
答:共组织了150人观看电影.

12. (2024·镜湖区一模)如图是今年 $ 1 $ 月的月历表,用矩形方框按如图所示的方法任意圈出 $ 4 $ 个数,请解答下列问题:
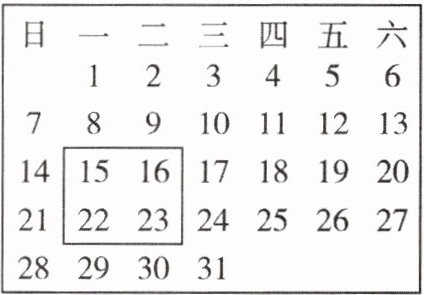
(1) 若方框中最大数与最小数的乘积为 $ 180 $,求最小数;
(2) 方框中最大数与最小数的乘积与这四个数的和能为 $ 124 $ 吗? 若能,求最小数;若不能,请说明理由.

答案： 12.
(1)设最小数是x,则最大数是x+8,
根据题意得:x(x+8)=180,
整理得:x²+8x−180=0,
解得:x₁=10,x₂=−18(不符合题意,舍去).
答:最小数是10;
(2)方框中最大数与最小数的乘积与这四个数的和不能为124,理由如下：
假设方框中最大数与最小数的乘积与这四个数的和能为124,设最小数是y,则另外三个数分别是y+1,y+7,y+8,
根据题意得:y(y+8)+y+y+1+y+7+y+8=124,
整理得:y²+12y−108=0,
解得:y₁=6,y₂=−18(不符合题意,舍去),
∵y=6在最后一列,
∴假设不成立,
即方框中最大数与最小数的乘积与这四个数的和不能为124.