《2025年顶尖课课练九年级数学下册人教版》

16. 若关于x的方程2x² - (4k + 1)x + 2k² - 1 = 0，x² - 2(k + 1)x + k² - 2 = 0，x² - (2k + 1)x + (k - 2)² = 0中至少有一个方程有实数根，求k的取值范围。

答案： k ≥ -$\frac{3}{2}$

17. 给出如下定义：如果a + b = 2，那么称a与b是关于1的“平衡数”。若(m + $\sqrt{3}$)(1 - $\sqrt{3}$) = −5 + 3$\sqrt{3}$，判断m + $\sqrt{3}$与5 - $\sqrt{3}$是不是关于1的“平衡数”，并说明理由。

答案： 不是，理由略

18. 若函数y = ax² - x + 1(a为常数)的图象与x轴只有一个交点，则a满足(　　　)。
A. a = $\frac{1}{4}$
B. a ≤ $\frac{1}{4}$
C. a = 0或a = -$\frac{1}{4}$
D. a = 0或a = $\frac{1}{4}$

答案： D

19. 小明利用计算机软件绘制函数y = $\frac{ax}{(x + 6)²}$(a，b为常数)的图象如图Z4 - 1所示，由学习函数的经验，可以推断常数a，b的值满足(　　　)。

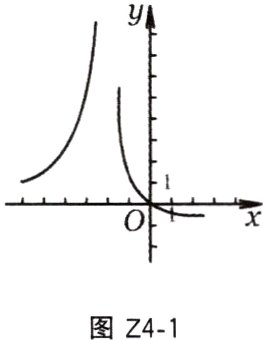
A. a＞0，b＞0
B. a＞0，b＜0
C. a＜0，b＞0
D. a＜0，b＜0

答案： C

20. 判断下列语句，正确的写上“真命题”，错误的请举一反例。
(1) 如果a＞b，那么a²＞b²；
(2) 如果a＞b＞0，那么a²＞b²；
(3) 如果a＜b，那么a²＜b²；
(4) 如果a＜b＜0，那么a²＞b²；
(5) 如果a，b都是无理数，那么ab也是无理数。

答案： 略