《2025年课时训练九年级数学下册人教版江苏人民出版社》

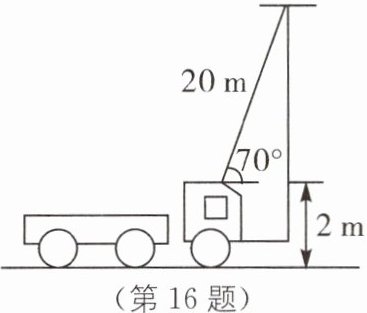
16［情境创新类问题］（2023·四平伊通模拟）如图所示，一辆消防车的梯子长20 m，并以70°倾斜于水平面. 如果这辆消防车的高度是2 m，求梯子可达的高度.（精确到0.01 m，参考数据：sin 70°≈0.939 7，cos 70°≈0.342 0，tan 70°≈2.747）

答案：
如图，连接$BC$。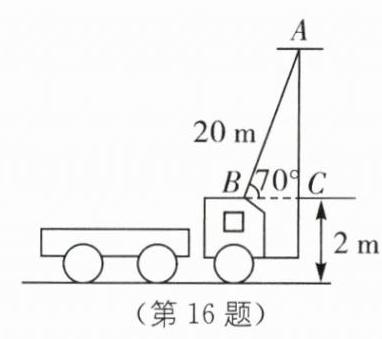
在$Rt\triangle ABC$中，$\angle ABC = 70^{\circ}$，$AB = 20$ m，$\sin\angle ABC=\frac{AC}{AB}$，所以$AC = AB\cdot\sin\angle ABC = 20\times\sin70^{\circ}\approx20\times0.9397\approx18.79$（m），所以梯子可达的高度约为$18.79 + 2 = 20.79$（m）。

17［情境创新类问题］鲁南高铁临沂段修建过程中需要经过一座小山. 如图，施工方计划沿AC方向开挖隧道，为了加快施工速度，要在小山的另一侧点D（点A，C，D共线）处同时施工. 测得∠CAB = 30°，AB = 4 km，∠ABD = 105°，求BD的长.

答案： 过点$B$作$BE\perp AD$于点$E$。因为$\angle CAB = 30^{\circ}$，$AB = 4$ km，所以$\angle ABE = 60^{\circ}$，$BE = 2$ km。因为$\angle ABD = 105^{\circ}$，所以$\angle EBD = 45^{\circ}$，所以$\angle EDB = 45^{\circ}$，所以$BE = DE = 2$（km），所以$BD=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$ km。即$BD$的长是$2\sqrt{2}$ km。

18（2023·湖北中考）为了防洪需要，某地决定新建一座拦水坝，如图，拦水坝的横断面为梯形ABCD，斜面坡度i = 3∶4是指坡面的铅直高度AF与水平宽度BF的比. 已知斜坡CD长度为20米，∠C = 18°，求斜坡AB的长.（结果精确到0.1米，参考数据：sin 18°≈0.31，cos 18°≈0.95，tan 18°≈0.32）

答案：
如图，过点$D$作$DE\perp BC$，垂足为$E$。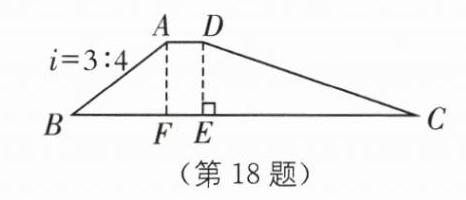
由题意，得$AF\perp BC$，$DE = AF$。因为斜面$AB$的坡度$i = 3:4$，所以$\frac{AF}{BF}=\frac{3}{4}$，设$AF = 3x$米，则$BF = 4x$米。在$Rt\triangle ABF$中，$AB=\sqrt{AF^{2}+BF^{2}}=\sqrt{(3x)^{2}+(4x)^{2}} = 5x$（米）。在$Rt\triangle DEC$中，$\angle C = 18^{\circ}$，$CD = 20$米，所以$DE = CD\cdot\sin18^{\circ}\approx20\times0.31 = 6.2$（米），所以$AF = DE = 6.2$米，$3x = 6.2$，解得$x=\frac{31}{15}$，所以$AB = 5x\approx10.3$（米），斜坡$AB$的长约为$10.3$米。