第65页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
15(2023·云南中考)如图,$BC$是$\odot O$的直径,$A$是$\odot O$上异于$B$,$C$的点. $\odot O$外的点$E$在射线$CB$上,直线$EA$与$CD$垂直,垂足为$D$,且$DA\cdot AC = DC\cdot AB$. 设$\triangle ABE$的面积为$S_{1}$,$\triangle ACD$的面积为$S_{2}$.
(1)判断直线$EA$与$\odot O$的位置关系,并证明你的结论;
(2)若$BC = BE$,$S_{2}=mS_{1}$,求常数$m$的值.

(1)判断直线$EA$与$\odot O$的位置关系,并证明你的结论;
(2)若$BC = BE$,$S_{2}=mS_{1}$,求常数$m$的值.

答案:
(1)证明\(AE\)与圆O相切: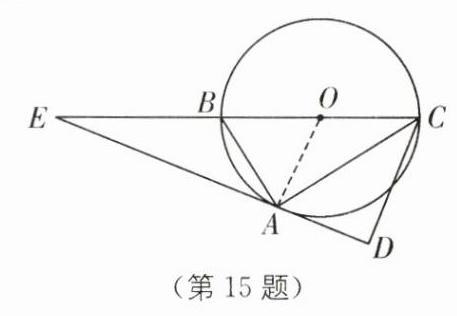
连接\(OA\),由\(DA\cdot AC = DC\cdot AB\)可得\(\frac{DA}{DC}=\frac{AB}{CA}\)。因为\(BC\)是圆O的直径,所以\(\angle BAC = 90^{\circ}=\angle ADC\),\(\triangle ABC\sim\triangle DAC\),\(\angle ACB=\angle ACD\)。又\(OA = OC\),所以\(\angle OAC=\angle ACB=\angle ACD\),\(OA\parallel CD\),\(\angle OAE=\angle CDE = 90^{\circ}\),\(OA\perp DE\),\(OA\)为半径,所以\(AE\)与圆O相切。 - (2)因为\(OA\parallel CD\),所以\(\triangle AOE\sim\triangle DCE\),\(\frac{AO}{CD}=\frac{OE}{EC}\)。设\(BO = OC = OA = a\),则\(BC = 2a\),因为\(BC = BE = 2a\),所以\(S_{\triangle ABE}=S_{\triangle ABC}\),\(EO = 3a\),\(EC = 4a\),\(\frac{a}{CD}=\frac{3a}{4a}\),解得\(CD=\frac{4}{3}a\)。又因为\(\triangle ABC\sim\triangle DAC\),\(\frac{BC}{AC}=\frac{AC}{CD}\),\(AC^{2}=BC\cdot CD=\frac{8}{3}a^{2}\),\(\frac{S_{\triangle ACD}}{S_{\triangle ABC}}=(\frac{AC}{BC})^{2}=\frac{2}{3}\),\(S_{2}=\frac{2}{3}S_{1}\),\(m=\frac{2}{3}\)。
(1)证明\(AE\)与圆O相切:

连接\(OA\),由\(DA\cdot AC = DC\cdot AB\)可得\(\frac{DA}{DC}=\frac{AB}{CA}\)。因为\(BC\)是圆O的直径,所以\(\angle BAC = 90^{\circ}=\angle ADC\),\(\triangle ABC\sim\triangle DAC\),\(\angle ACB=\angle ACD\)。又\(OA = OC\),所以\(\angle OAC=\angle ACB=\angle ACD\),\(OA\parallel CD\),\(\angle OAE=\angle CDE = 90^{\circ}\),\(OA\perp DE\),\(OA\)为半径,所以\(AE\)与圆O相切。 - (2)因为\(OA\parallel CD\),所以\(\triangle AOE\sim\triangle DCE\),\(\frac{AO}{CD}=\frac{OE}{EC}\)。设\(BO = OC = OA = a\),则\(BC = 2a\),因为\(BC = BE = 2a\),所以\(S_{\triangle ABE}=S_{\triangle ABC}\),\(EO = 3a\),\(EC = 4a\),\(\frac{a}{CD}=\frac{3a}{4a}\),解得\(CD=\frac{4}{3}a\)。又因为\(\triangle ABC\sim\triangle DAC\),\(\frac{BC}{AC}=\frac{AC}{CD}\),\(AC^{2}=BC\cdot CD=\frac{8}{3}a^{2}\),\(\frac{S_{\triangle ACD}}{S_{\triangle ABC}}=(\frac{AC}{BC})^{2}=\frac{2}{3}\),\(S_{2}=\frac{2}{3}S_{1}\),\(m=\frac{2}{3}\)。
16 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 8$,$BC = 6$,$CD\perp AB$于点$D$. 点$P$从点$D$出发,沿线段$DC$向点$C$运动,点$Q$从点$C$出发,沿线段$CA$向点$A$运动. 两点同时出发. 速度都为每秒1个单位长度,当点$P$运动到$C$时,两点都停止. 设运动时间为$t$秒.
(1)求线段$CD$的长.
(2)设$\triangle CPQ$的面积为$S$,求$S$与$t$之间的函数解析式,并确定在运动过程中是否存在某一时刻$t$,使得$S_{\triangle CPQ}:S_{\triangle ABC}=9:100$? 若存在,求出$t$的值;若不存在,说明理由.

(1)求线段$CD$的长.
(2)设$\triangle CPQ$的面积为$S$,求$S$与$t$之间的函数解析式,并确定在运动过程中是否存在某一时刻$t$,使得$S_{\triangle CPQ}:S_{\triangle ABC}=9:100$? 若存在,求出$t$的值;若不存在,说明理由.

答案:
(1)因为\(\angle ACB = 90^{\circ}\),\(AC = 8\),\(BC = 6\),所以\(AB=\sqrt{AC^{2}+BC^{2}} = 10\)。由\(\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD\),可得\(\frac{1}{2}×8×6=\frac{1}{2}×10×CD\),解得\(CD = 4.8\)。 - (2)\(AD=\sqrt{AC^{2}-CD^{2}} = 6.4\)。过点Q作\(QH\perp CD\)于点H,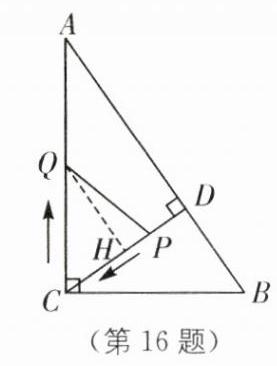
因为\(CD\perp AB\),所以\(QH\parallel AD\),\(\triangle CHQ\sim\triangle CDA\),\(\frac{QH}{AD}=\frac{CQ}{AC}\),即\(\frac{QH}{6.4}=\frac{t}{8}\),解得\(QH = 0.8t\),\(S=\frac{1}{2}QH\cdot CP=\frac{1}{2}×0.8t×(4.8 - t)=-0.4t^{2}+1.92t\)。又\(S_{\triangle ABC}=\frac{1}{2}AC\cdot BC = 24\),由\(S_{\triangle CPQ}:S_{\triangle ABC}=9:100\),可得\(\frac{-0.4t^{2}+1.92t}{24}=\frac{9}{100}\),整理得\(5t^{2}-24t + 27 = 0\),解得\(t_{1}=3\),\(t_{2}=1.8\),即在运动过程中存在某一时刻\(t\),使\(S_{\triangle CPQ}:S_{\triangle ABC}=9:100\),\(t\)值为3或1.8。
(1)因为\(\angle ACB = 90^{\circ}\),\(AC = 8\),\(BC = 6\),所以\(AB=\sqrt{AC^{2}+BC^{2}} = 10\)。由\(\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD\),可得\(\frac{1}{2}×8×6=\frac{1}{2}×10×CD\),解得\(CD = 4.8\)。 - (2)\(AD=\sqrt{AC^{2}-CD^{2}} = 6.4\)。过点Q作\(QH\perp CD\)于点H,

因为\(CD\perp AB\),所以\(QH\parallel AD\),\(\triangle CHQ\sim\triangle CDA\),\(\frac{QH}{AD}=\frac{CQ}{AC}\),即\(\frac{QH}{6.4}=\frac{t}{8}\),解得\(QH = 0.8t\),\(S=\frac{1}{2}QH\cdot CP=\frac{1}{2}×0.8t×(4.8 - t)=-0.4t^{2}+1.92t\)。又\(S_{\triangle ABC}=\frac{1}{2}AC\cdot BC = 24\),由\(S_{\triangle CPQ}:S_{\triangle ABC}=9:100\),可得\(\frac{-0.4t^{2}+1.92t}{24}=\frac{9}{100}\),整理得\(5t^{2}-24t + 27 = 0\),解得\(t_{1}=3\),\(t_{2}=1.8\),即在运动过程中存在某一时刻\(t\),使\(S_{\triangle CPQ}:S_{\triangle ABC}=9:100\),\(t\)值为3或1.8。
17(2023·常德模拟)如图,点$E$是正方形$ABCD$中边$BC$上一点. 将$\triangle ABE$沿$AE$翻折得到$\triangle AGE$. 使点$B$落在点$G$处,延长$AG$与边$CD$交于点$H$,直线$EG$与$CD$交于点$F$.
(1)如图(1),求证:$DF = GF$;
(2)如图(2),若直线$EG$与$AD$的延长线交于点$N$. 求证:$AD\cdot FN = AN\cdot DF$;
(3)如图(3),若直线$EG$与$AB$,$AD$的延长线分别交于点$M$,$N$,$AG$交$BD$于点$P$. 求证:$\frac{BP}{DP}=\frac{AM}{AN}$.


(1)如图(1),求证:$DF = GF$;
(2)如图(2),若直线$EG$与$AD$的延长线交于点$N$. 求证:$AD\cdot FN = AN\cdot DF$;
(3)如图(3),若直线$EG$与$AB$,$AD$的延长线分别交于点$M$,$N$,$AG$交$BD$于点$P$. 求证:$\frac{BP}{DP}=\frac{AM}{AN}$.


答案:
(1)连接\(AF\),因为四边形\(ABCD\)是正方形,所以\(AB = AD\),\(\angle B=\angle D = 90^{\circ}\)。将\(\triangle ABE\)沿\(AE\)翻折得到\(\triangle AGE\),所以\(AB = AG\),\(\angle AGE=\angle B = 90^{\circ}\),\(AD = AG\),\(\angle D=\angle AGF = 90^{\circ}\),又\(AF = AF\),所以\(Rt\triangle ADF\cong Rt\triangle AGF(HL)\),\(DF = GF\)。 - (2)因为\(\angle ADC=\angle AGN = 90^{\circ}\),所以\(\angle N+\angle NFD=\angle N+\angle NAG = 90^{\circ}\),\(\angle NAG=\angle NFD\),又\(\angle FDN=\angle AGN = 90^{\circ}\),所以\(\triangle NAG\sim\triangle NFD\),\(\frac{AN}{NF}=\frac{AG}{DF}\),因为\(AD = AG\),所以\(AD\cdot NF = AN\cdot DF\)。 - (3)因为\(AB\parallel CD\),所以\(\triangle ABP\sim\triangle HDP\),\(\frac{AB}{DH}=\frac{BP}{DP}=\frac{AD}{DH}\)。因为\(\angle AHD+\angle NAG = 90^{\circ}=\angle N+\angle NAG\),所以\(\angle N=\angle AHD\),又\(\angle ADH=\angle MAN = 90^{\circ}\),所以\(\triangle MAN\sim\triangle ADH\),\(\frac{AM}{AN}=\frac{AD}{DH}\),所以\(\frac{BP}{DP}=\frac{AM}{AN}\)。
查看更多完整答案,请扫码查看


