《2025年课时训练九年级数学下册人教版江苏人民出版社》

1（2023·抚顺东洲区模拟）观察下列图形，下列各组图形不是相似图形的是( ).

答案： B

2 下列四组图形中，相似图形为( ).

答案： B

3 若△ABC的每条边长增加各自的10％得到△A'B'C'，则∠B'的度数与其对应角∠B的度数相比( ).
A. 增加了10％
B. 减少了10％
C. 增加了(1+10％)
D. 没有改变

答案： D

4 下列说法：①所有的等腰三角形都相似；②所有的正三角形都相似；③所有的正方形都相似；④所有的矩形都相似；⑤所有的圆都相似. 其中说法正确的序号是_______.

答案： ②③⑤

5 利用复印机的缩放功能，将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形，那么放大前后的两个三角形的周长比是_______.

答案： 1 : 4

6 如图，利用右边的格子图，把左边图中奔跑的小人放大一倍.

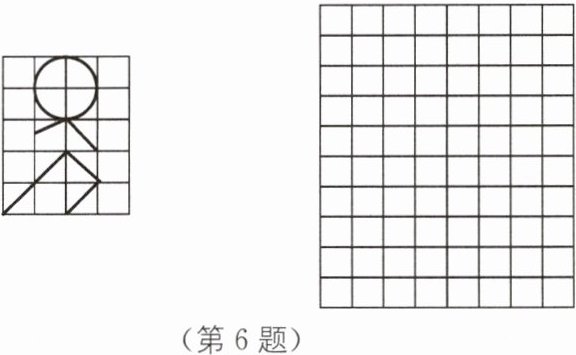
答案：
如图所示.  （第6题）

7 在右边的网格纸中描出左边图形缩小为原图一半的图形.

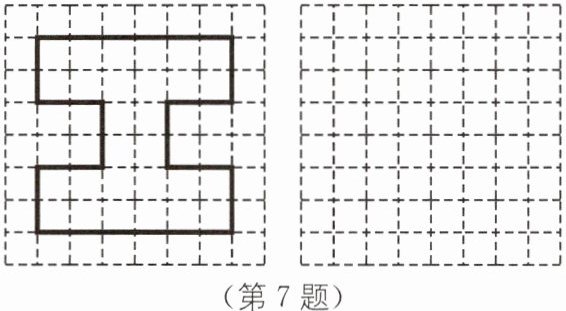
答案：
如图所示. （第7题）

8（2023·四川遂宁射洪期末）有四组线段，每组线段长度如下：①2，1，$\sqrt{2}$，$\sqrt{2}$；②3，2，6，4；③$\frac{1}{2}$，1，$\sqrt{5}$，$\sqrt{2}$；④1，3，5，7. 其中能组成比例的有( ).
A. ①③
B. ①②
C. ①②③
D. ②③④

答案： B

9（2023·上海宝山区一模）已知线段a = 2，b = 8，如果线段c是a，b的比例中项，那么c = _______.

答案： 4

10 我们知道：如果$\frac{a}{b}=\frac{c}{d}$，且b + d≠0，那么$\frac{a}{b}=\frac{c}{d}=\frac{a + c}{b + d}$.
（1）若b + d = 0，则a，c满足什么关系？
（2）若$\frac{b + c}{a}=\frac{a + c}{b}=\frac{a + b}{c}=t$，求$t^{2}-t - 2$的值.

答案：
(1) 因为$\frac{a}{b}=\frac{c}{d}$，$b + d = 0$，所以$\frac{a}{-d}=\frac{c}{d}$。 所以$a = -c$，即$a + c = 0$。
(2) ①当$a + b + c\neq0$时， $\frac{b + c}{a}=\frac{a + c}{b}=\frac{a + b}{c}=t=\frac{2(a + b + c)}{a + b + c}=2$， 所以$t^{2}-t - 2=2^{2}-2 - 2 = 0$； ②当$a + b + c = 0$时，$\frac{b + c}{a}=\frac{a + c}{b}=\frac{a + b}{c}=t=-1$， 所以$t^{2}-t - 2 = 0$。 综上，$t^{2}-t - 2$的值为0。