《2025年课时训练九年级数学下册人教版江苏人民出版社》

13 某数学兴趣小组要测量实验大楼部分楼体的高度(如图(1)所示，CD部分)，在起点A处测得大楼部分楼体CD的顶端C点的仰角为45°，底端D点的仰角为30°，在同一剖面沿水平地面向前走20米到达B处，测得顶端C的仰角为63.4°(如图(2)所示)，求大楼部分楼体CD的高度约为多少米？(结果精确到1米，参考数据：sin63.4°≈0.89，cos63.4°≈0.45，tan63.4°≈2.00，$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73)

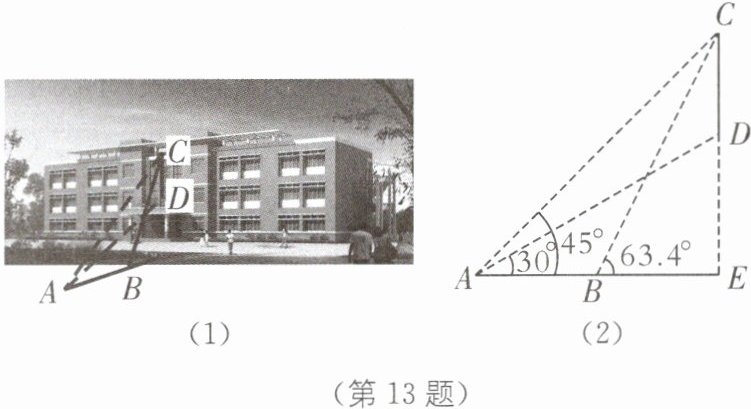
(1) (2)
(第13题)

答案： 设楼高CE为x米. 在Rt△AEC中，∠CAE = 45°，
∴AE = CE = x.
∵AB = 20米，
∴BE = (x - 20)米. 在Rt△CEB中，CE = BE·tan63.4°≈2(x - 20)米， 即2(x - 20)=x，解得x = 40. 在Rt△DAE中，$DE = AE\cdot\tan30^{\circ}=40\times\frac{\sqrt{3}}{3}=\frac{40\sqrt{3}}{3}$，
∴$CD = CE - DE = 40-\frac{40\sqrt{3}}{3}\approx17$(米)， 故大楼部分楼体CD的高度约为17米.

14 为加快城乡对接，建设全域美丽乡村，某地区对A，B两地间的公路进行改建. 如图，A，B两地之间有一座山，汽车原来从A地到B地需途经C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶. 已知BC = 80千米，∠A = 45°，∠B = 30°.
(1)开通隧道前，汽车从A地到B地大约要走多少千米？
(2)开通隧道后，汽车从A地到B地大约可以少走多少千米？(结果精确到0.1千米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73)

(第14题)

答案：

(1)如图，过点C作AB的垂线CD，垂足为D.! 
∵AB⊥CD，$\sin30^{\circ}=\frac{CD}{BC}$，BC = 80千米，
∴$CD = BC\cdot\sin30^{\circ}=80\times\frac{1}{2}=40$(千米)，
∴$AC=\frac{CD}{\sin45^{\circ}}=\frac{40}{\frac{\sqrt{2}}{2}} = 40\sqrt{2}$(千米)，
∴$AC + BC = 80 + 40\sqrt{2}\approx136.4$(千米). 故开通隧道前，汽车从A地到B地大约要走136.4千米.
(2)在Rt△BCD中，$\cos30^{\circ}=\frac{BD}{BC}$，BC = 80千米，
∴$BD = BC\cdot\cos30^{\circ}=80\times\frac{\sqrt{3}}{2}=40\sqrt{3}$(千米). 在Rt△ACD中，$\tan45^{\circ}=\frac{CD}{AD}$，CD = 40千米，
∴$AD=\frac{CD}{\tan45^{\circ}}=\frac{40}{1}=40$(千米)，
∴$AB = AD + BD = 40 + 40\sqrt{3}\approx109.2$(千米)，
∴汽车从A地到B地比原来少走的路程为AC + BC - AB = 136.4 - 109.2 = 27.2(千米). 故汽车从A地到B地比原来大约可以少走27.2千米.

15 如图，在一座山的前方有一栋住宅，已知山高AB = 120 m，楼高CD = 99 m，某天上午9时太阳光线从山顶点A处照射到住宅的点E处. 在点A处测得点E的俯角∠EAM = 45°，上午10时太阳光线从山顶点A处照射到住宅点F处，在点A处测得点F的俯角∠FAM = 60°，已知每层楼的高度为3 m，EF = 40 m. 问：以当天测量数据为依据，不考虑季节天气变化，至少要买该住宅的第几层楼，才能使上午10时太阳光线照射到该层楼的外墙？($\sqrt{3}$≈1.73)

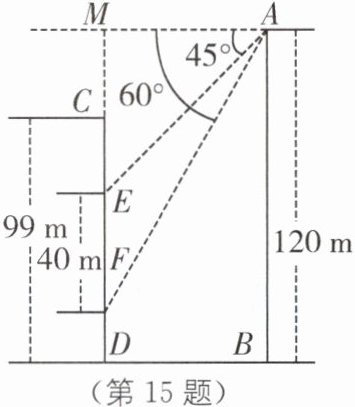
(第15题)

答案： 根据题意可知，四边形ABDM是矩形，
∴AB = MD = 120 m. 在Rt△AME中，ME = AM·tan45° = AM. 在Rt△AMF中，MF = AM·tan60°=$\sqrt{3}AM$.
∵EF = MF - ME = 40 m，
∴$\sqrt{3}AM - AM = 40$，
∴$AM = 20(\sqrt{3}+1)$m，
∴$MF=(60 + 20\sqrt{3})$m，
∴$DF = 120-(60 + 20\sqrt{3})\approx25.4$(m)，
∵25.4÷3≈8.5.
∴至少要买该住宅的第9层楼，才能使上午10时太阳光线照射到该层楼的外墙.