《2025年课时训练九年级数学下册人教版江苏人民出版社》

1. 如图，在正方形 $ABCD$ 中，$E$ 为 $AB$ 的中点，$AF\perp DE$ 于点 $O$，则 $\frac{AO}{DO}$ 等于（ ）.

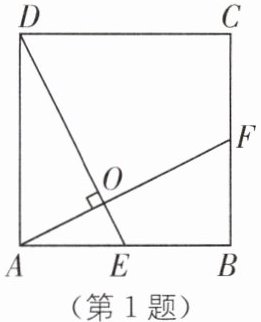
A. $\frac{2\sqrt{5}}{3}$
B. $\frac{1}{3}$
C. $\frac{2}{3}$
D. $\frac{1}{2}$

答案： D

2. 如图，在一块斜边长 $30\ cm$ 的直角三角形木板（$Rt\triangle ACB$）上截取一个正方形 $CDEF$，点 $D$ 在边 $BC$ 上，点 $E$ 在斜边 $AB$ 上，点 $F$ 在边 $AC$ 上，若 $AF:AC = 1:3$，则这块木板截取正方形 $CDEF$ 后，剩余部分的面积为（ ）.

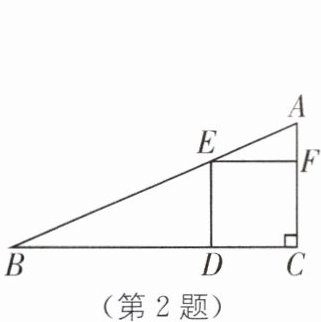
A. $100\ cm^{2}$
B. $150\ cm^{2}$
C. $170\ cm^{2}$
D. $200\ cm^{2}$

答案： A

3. [传统文化]《九章算术》中记载了一种测量井深的方法. 如图，在井口 $B$ 处立一根垂直于井口的木杆 $BD$，从木杆的顶端点 $D$ 观察井内水岸点 $C$，视线 $DC$ 与井口的直径 $AB$ 交于点 $E$. 如果测得 $AB = 1.8$ 米，$BD = 1$ 米，$BE = 0.2$ 米. 请求出井深 $AC$ 的长.

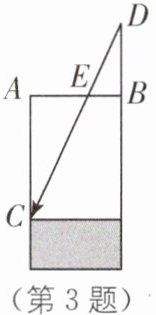
答案： 由题意，得BD//AC，所以△BDE∽△ACE。 所以$\frac{BD}{BE}=\frac{AC}{AE}$，即$\frac{1}{0.2}=\frac{AC}{1.8 - 0.2}$， 解得AC = 8米。故井深AC的长为8米。

4. 如图，小芳和爸爸正在散步，爸爸身高 $1.8\ m$，他在地面上的影长为 $2.1\ m$. 若小芳比爸爸矮 $0.3\ m$，则她的影长为（ ）.

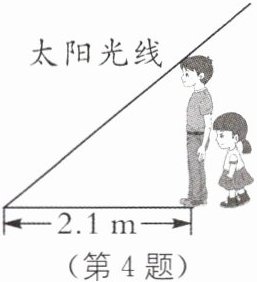
A. $1.3\ m$
B. $1.65\ m$
C. $1.75\ m$
D. $1.8\ m$

答案： C

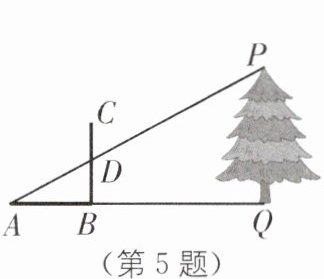
5. [传统文化](2023·江西中考)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺（即图中的 $ABC$）.“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度. 如图，点 $A$，$B$，$Q$ 在同一水平线上，$\angle ABC$ 和 $\angle AQP$ 均为直角，$AP$ 与 $BC$ 相交于点 $D$. 测得 $AB = 40\ cm$，$BD = 20\ cm$，$AQ = 12\ m$，则树高 $PQ=$_______$m$.

答案： 6

6. 在同一时刻，物体的高度与它的影长成正比，在某一时刻，有人测得一高为 $1.8$ 米的竹竿的影长为 $3$ 米，某一高楼的影长为 $60$ 米，那么高楼的高度为_______.

答案： 36米

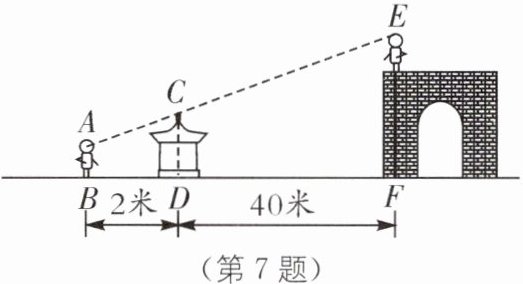
7. (2023·陕西商洛商南期末)某天小明站在地面上给站在城楼上的小亮照相时发现：他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上（如图）. 已知小明的眼睛离地面的距离 $AB = 1.6$ 米，凉亭顶端离地面的距离 $CD = 2$ 米，小明到凉亭的距离 $BD = 2$ 米，凉亭离城楼底部的距离 $DF = 40$ 米，小亮身高 $1.75$ 米. 请根据以上数据求出城楼的高度.

答案：
如图，过点A作AM⊥EF于点M，交CD于点N。 依题意，得AN = 2米，CN = 2 - 1.6 = 0.4（米），MN = 40米， 所以AM = AN + MN = 42（米）。 因为CN//EM，所以△ACN∽△AEM，所以$\frac{CN}{EM}=\frac{AN}{AM}$， 即$\frac{0.4}{EM}=\frac{2}{42}$，解得EM = 8.4米。 因为AB = MF = 1.6米， 所以城楼的高度为8.4 + 1.6 - 1.75 = 8.25（米）。