《2025年课时训练九年级数学下册人教版江苏人民出版社》

9 在平面直角坐标系中，点$A$的坐标是$(-2,1)$，以原点$O$为位似中心，把线段$OA$放大为原来的$2$倍，点$A$的对应点为$A'$. 若点$A'$恰在某一反比例函数图象上，则该反比例函数解析式为________.

答案： $y = -\frac{8}{x}$

10 已知$\triangle ABC$在坐标平面内三顶点的坐标分别为$A(0,2)$，$B(3,3)$，$C(2,1)$. 以$B$为位似中心，画出$\triangle A_{1}B_{1}C_{1}$与$\triangle ABC$相似，两三角形位于点$B$同侧且相似比是$3$，则点$C$的对应顶点$C_{1}$的坐标是________.

答案： （0，-3）

11 如图，$\triangle ABC$的顶点坐标分别为$A(-2,0)$，$B(0,\frac{1}{2})$，$C(1,2)$，画出它的两个以原点$O$为位似中心，相似比为$2$的位似图形，并求出各顶点的坐标.

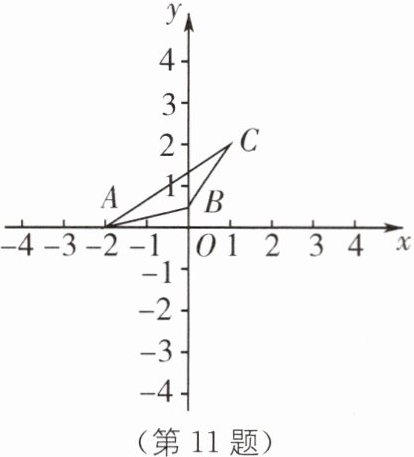
答案： 答案：画图略. （1）当位似图形在位似中心的同侧时，△ABC的位似图形△A′B′C′的各顶点的坐标是△ABC对应顶点坐标的2倍，即A′（-4，0），B′（0，1），C′（2，4）. （2）当位似图形在位似中心的两侧时，△ABC的位似图形△A″B″C″的各顶点的坐标是△ABC对应顶点坐标的 -2倍，即A″（4，0），B″（0，-1），C″（-2，-4）.

12 (2023·西安灞桥区铁一中滨河学校模拟)$\triangle ABC$在平面直角坐标系中的位置如图所示，网格中每个小正方形的边长都是$1$个单位长度.
(1)请画出$\triangle ABC$关于$x$轴对称的$\triangle A_{1}B_{1}C_{1}$，点$A$，$B$，$C$的对应点分别为$A_{1}$，$B_{1}$，$C_{1}$；
(2)请以原点$O$为位似中心，在第四象限内画一个$\triangle A_{2}B_{2}C_{2}$，使它与$\triangle ABC$的相似比为$2:1$.

答案：
答案：（1）如图，△A₁B₁C₁即为所求. （2）如图，△A₂B₂C₂即为所求. 

13 (2023·广西北海银海区外国语实验学校期末)如图，$\triangle ABC$的三个顶点坐标分别为$A(-2,4)$，$B(-3,1)$，$C(-1,1)$，以坐标原点$O$为位似中心，相似比为$2$，在第二象限内将$\triangle ABC$放大，放大后得到$\triangle A'B'C'$.
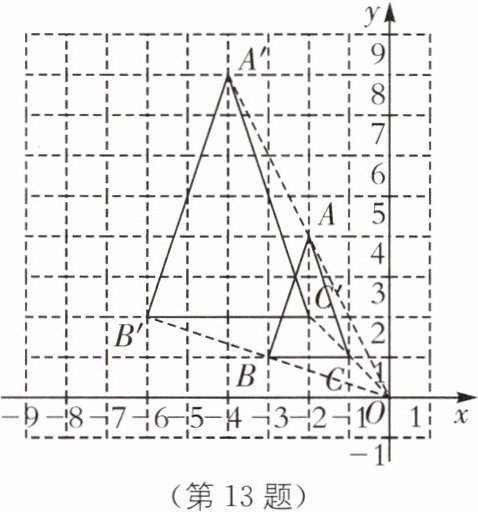
(1)写出点$A'$，$B'$，$C'$的坐标(点$A$，$B$，$C$的对应点分别为$A'$，$B'$，$C'$)；
(2)求$\triangle A'B'C'$与$\triangle ABC$的周长比.

答案： 答案：（1）
∵以坐标原点O为位似中心，相似比为2，在第二象限内将△ABC放大，A（-2，4），B（-3，1），C（-1，1），
∴点A′的坐标为（-2×2，4×2），B′的坐标为（-3×2，1×2），C′的坐标为（-1×2，1×2），
∴点A′的坐标为（-4，8），B′的坐标为（-6，2），C′的坐标为（-2，2）. （2）根据相似三角形的周长比等于相似比，
∴△A′B′C′与△ABC的周长比为2.