《2025年课时训练九年级数学下册人教版江苏人民出版社》

1. 反比例函数$y = \frac{k}{x}$的图象上有一点$P(2,n)$，将点$P$向右平移$1$个单位，再向下平移$1$个单位得到点$Q$，若点$Q$也在该函数的图象上，则$k =$_______.

答案： 6

2. 如图，菱形$OBAC$的顶点$A$在反比例函数$y = \frac{k}{x}(x＞0)$的图象上，点$B$在$y$轴上，点$C$的坐标为$(4,3)$.
- （1）求$k$的值；
- （2）点$P$为反比例函数图象上一个动点，过点$P$作$PN\perp x$轴于点$N$，交$OA$于点$M$，若$PM = MN$，求点$P$的坐标.

答案： （1）如图，过点C作x轴的垂线，垂足为F。 ![img id=第2题] 因为点C的坐标为(4,3)，所以OF = 4，CF = 3，由此可得OC = 5，AC = 5，那么点A的坐标为(4,8)。 由于顶点A在反比例函数$y=\frac{k}{x}(x ＞ 0)$的图象上，所以k = xy = 4×8 = 32。 （2）由（1）可知，反比例函数解析式为$y=\frac{32}{x}$。 设直线OA的解析式为y = k₁x，将A(4,8)代入，可得4k₁ = 8，解得k₁ = 2，所以直线OA的解析式为y = 2x。 设N点坐标为(m,0)，则M点坐标为(m,2m)，P点坐标为$(m,\frac{32}{m})$。因为PM = MN，所以P(m,4m)，则$\frac{32}{m}=4m$，解得m = $2\sqrt{2}$（负值舍去），所以P($2\sqrt{2},8\sqrt{2}$)。

5. 已知$(x_1,y_1)$，$(x_2,y_2)$，$(x_3,y_3)$为双曲线$y = -\frac{3}{x}$上的三个点，且$x_1＜x_2＜x_3$，则以下判断正确的是（ ）.
A. 若$x_1x_2＞0$，则$y_2y_3＞0$
B. 若$x_1x_3＞0$，则$y_2y_3＜0$
C. 若$x_1x_3＜0$，则$y_2y_3＞0$
D. 若$x_1x_2＜0$，则$y_1y_3＜0$

答案： [解析]因为反比例函数$y=-\frac{3}{x}$中k = -3 ＜ 0，所以函数图象在第二、四象限，在每一象限内，y随x的增大而增大。 若x₁x₂ ＞ 0，当x₁ ＜ x₂ ＜ 0 ＜ x₃时，y₃ ＜ 0 ＜ y₁ ＜ y₂，则y₂y₃ ＜ 0，故A不符合题意； 若x₁x₃ ＞ 0，即x₁，x₂，x₃同号，有y₁，y₂，y₃同号，则y₂y₃ ＞ 0，故B不符合题意； 若x₁x₃ ＜ 0，当x₁ ＜ x₂ ＜ 0 ＜ x₃时，y₃ ＜ 0 ＜ y₁ ＜ y₂，则y₂y₃ ＜ 0，故C不符合题意； 若x₁x₂ ＜ 0，即x₁ ＜ 0 ＜ x₂ ＜ x₃，有y₂ ＜ y₃ ＜ 0 ＜ y₁，则y₁y₃ ＜ 0，故D符合题意。故选D。

6. 如图是反比例函数$y = \frac{2n - 4}{x}$的图象的一支，根据图象回答下列问题：
- （1）图象的另一支在哪个象限？常数$n$的取值范围是什么？
- （2）若函数图象经过点$(3,1)$，求$n$的值.
- （3）在这个函数图象的某一支上任取点$A(a_1,b_1)$和点$B(a_2,b_2)$，如果$a_1＜a_2$，试比较$b_1$和$b_2$的大小.

答案： （1）图象的另一支在第三象限。 由图象可知，2n - 4 ＞ 0，解得n ＞ 2。 （2）将点(3,1)代入$y=\frac{2n - 4}{x}$，可得$1=\frac{2n - 4}{3}$，解得$n=\frac{7}{2}$。 （3）因为2n - 4 ＞ 0，所以在这个函数图象的任一支上，y都随x增大而减小。所以当a₁ ＜ a₂时，b₁ ＞ b₂。

3. （2022·广东中考）点$(1,y_1)$，$(2,y_2)$，$(3,y_3)$，$(4,y_4)$在反比例函数$y = \frac{4}{x}$图象上，则$y_1$，$y_2$，$y_3$，$y_4$中最小的是（ ）.
A. $y_1$
B. $y_2$
C. $y_3$
D. $y_4$

答案： [解析]因为k = 4 ＞ 0，所以在第一象限内，y随x的增大而减小。 因为(1,y₁)，(2,y₂)，(3,y₃)，(4,y₄)在反比例函数$y=\frac{4}{x}$图象上，且1 ＜ 2 ＜ 3 ＜ 4，所以y₄最小。故选D。 ■知识拓展 在反比例函数中，已知各点的横坐标，比较纵坐标的大小，首先应区分各点是否在同一象限内。在同一象限内，按同一象限内点的特点来比较，不在同一象限内，按坐标系内点的特点来比较。

4. （2023·通辽中考）已知点$A(x_1,y_1)$，$B(x_2,y_2)$在反比例函数$y = -\frac{2}{x}$的图象上，且$x_1＜0＜x_2$，则下列结论一定正确的是（ ）.
A. $y_1 + y_2＜0$
B. $y_1 + y_2＞0$
C. $y_1 - y_2＜0$
D. $y_1 - y_2＞0$

答案： D

7. （2023·湖南怀化期末）如图，点$A$在双曲线$y = \frac{k}{x}$上，$AB\perp y$轴于$B$，$S_{\triangle AOB}=3$，则$k =$（ ）.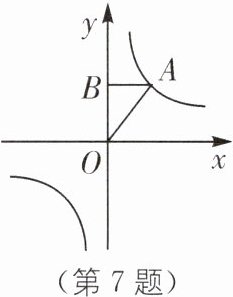
A. 3
B. 6
C. 18
D. 不能确定

答案： B

8. （2023·绥化中考）在平面直角坐标系中，点$A$在$y$轴的正半轴上，$AC$平行于$x$轴，点$B$，$C$的横坐标都是$3$，$BC = 2$，点$D$在$AC$上，且其横坐标为$1$，若反比例函数$y = \frac{k}{x}(x＞0)$的图象经过点$B$，$D$，则$k$的值是（ ）.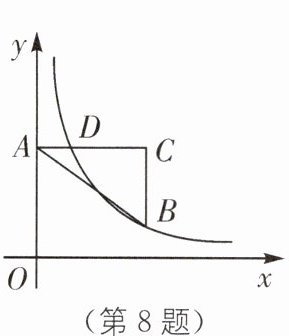
A. 1
B. 2
C. 3
D. $\frac{3}{2}$

答案： C[解析]因为点A在y轴正半轴上，AC//x轴，点B、C的横坐标都是3，且BC = 2，点D在AC上，且横坐标为1，所以设B(3,a)，则D(1,a + 2)。 因为反比例函数$y=\frac{k}{x}(x ＞ 0)$的图象经过点B，D，所以3a = a + 2，解得a = 1，所以B(3,1)，则k = 3×1 = 3。故选C。