《2025年课时训练九年级数学下册人教版江苏人民出版社》

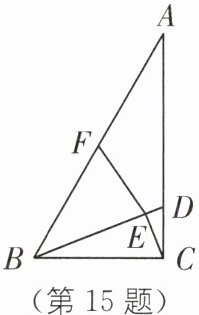
15. （2023·池州贵池区二模）如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\angle A = 30^{\circ}$，$BC = 6$，$D$为$AC$上任意一点，$F$为$AB$的中点，连接$BD$，$E$在$BD$上且$\angle BEC = 90^{\circ}$，连接$EF$，则$EF$的最小值为（ ）.

A. $\frac{3\sqrt{3}-3}{2}$
B. $2\sqrt{3}-3$
C. $3\sqrt{3}-3$
D. $3$

答案：
**解析**：如图，取BC的中点Q，连接EQ，FQ。因为F为AB的中点，所以$FQ=\frac{1}{2}AC$。 - 因为∠ACB = 90°，∠A = 30°，BC = 6，所以$AC=\frac{BC}{\tan A}=\frac{6}{\frac{\sqrt{3}}{3}}=6\sqrt{3}$，所以$FQ = 3\sqrt{3}$。 - 因为∠BEC = 90°，所以$EQ=\frac{1}{2}BC = 3$。当E，F，Q三点共线的时候，EF的值最小，所以$EF = FQ - EQ = 3\sqrt{3}-3$。故选C。

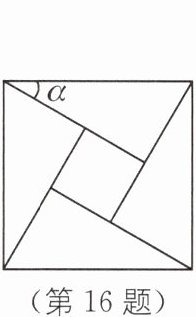
16. [传统文化]（2023·内蒙古中考）如图源于我国汉代数学家赵爽的弦图，它是由四个全等直角三角形与一个小正方形拼成的一个大正方形. 若小正方形的面积为$1$，大正方形的面积为$25$，直角三角形中较小的锐角为$\alpha$，则$\cos\alpha$的值为（ ）.

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$

答案： **解析**：因为小正方形的面积为1，大正方形的面积为25，所以小正方形的边长为1，大正方形的边长为5。 - 设直角三角形较短的直角边为a，则较长的直角边为$a + 1$，其中$a＞0$，由勾股定理，得$a^{2}+(a + 1)^{2}=5^{2}$，解得$a = 3$（负值舍去），所以$a + 1 = 4$，所以$\cos\alpha=\frac{4}{5}$。故选D。 - **解题技巧**：解题的关键是准确识图，熟练掌握锐角三角函数的定义，通过设置适当的未知数，利用勾股定理构造方程求出三角形的边。

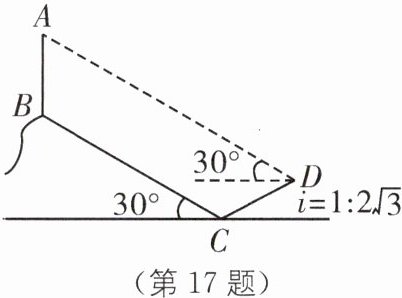
17. 如图，在高度为$100$米的小山上竖直建有一座铁塔，小明为测得铁塔的高度，先在山脚$C$处测得铁塔底部$B$的仰角为$30^{\circ}$，后沿坡度$i = 1:2\sqrt{3}$的山坡向上行走$10\sqrt{13}$米到达点$D$处，在点$D$处测得铁塔顶部$A$的仰角为$30^{\circ}$，求铁塔$AB$的高度.

答案：
如图，延长AB交地面于点E，过点D分别作DG⊥AE于点G，作DF⊥EC于点F，则四边形DFEG是矩形，所以DG = EF，DF = EG。 - 由题意，得BE = 100米，$CD = 10\sqrt{13}$米，在Rt△BCE中，$\tan\angle BCE=\frac{BE}{CE}$，所以$CE=\frac{BE}{\tan30^{\circ}}=\frac{100}{\frac{\sqrt{3}}{3}}=100\sqrt{3}$（米）。 - 在Rt△CDF中，因为$DF:CF = 1:2\sqrt{3}$，所以$CF = 2\sqrt{3}DF$。因为$DF^{2}+CF^{2}=CD^{2}$，所以$DF^{2}+(2\sqrt{3}DF)^{2}=(10\sqrt{13})^{2}$，所以DF = 10米，$CF = 20\sqrt{3}$米。所以$DG = EF = CE + CF = 120\sqrt{3}$米，$EG = DF = 10$米。 - 在Rt△ADG中，因为$\tan\angle ADG=\frac{AG}{DG}$，所以$AG = DG\cdot\tan30^{\circ}=120\sqrt{3}\times\frac{\sqrt{3}}{3}=120$（米）。所以$AB = AG + EG - BE = 120 + 10 - 100 = 30$（米）。故铁塔AB的高度为30米。!

18. [情境创新类问题]（2023·河南中考）综合实践活动中，某小组用木板自制了一个测高仪测量树高，测高仪$ABCD$为正方形，$AB = 30\ cm$，顶点$A$处挂了一个铅锤$M$. 如图是测量树高的示意图，测高仪上的点$D$，$A$与树顶$E$在一条直线上，铅垂线$AM$交$BC$于点$H$. 经测量，点$A$距地面$1.8\ m$，到树$EG$的距离$AF = 11\ m$，$BH = 20\ cm$. 求树$EG$的高度.（结果精确到$0.1\ m$）

答案： 由题意可知，∠BAE = ∠MAF = 90°，FG = 1.8 m，则∠EAF + ∠BAF = ∠BAF + ∠BAH = 90°，所以∠EAF = ∠BAH。 - 在Rt△ABH中，AB = 30 cm，BH = 20 cm，则$\tan\angle BAH=\frac{BH}{AB}=\frac{2}{3}$。 - 所以在Rt△AFE中，$\tan\angle EAF=\frac{EF}{AF}=\tan\angle BAH=\frac{2}{3}$。因为AF = 11 m，则$\frac{EF}{11}=\frac{2}{3}$，所以$EF=\frac{22}{3}$m，所以$EG = EF + FG=\frac{22}{3}+1.8\approx9.1$（m）。故树EG的高度为9.1 m。