《2025年课时训练九年级数学下册人教版江苏人民出版社》

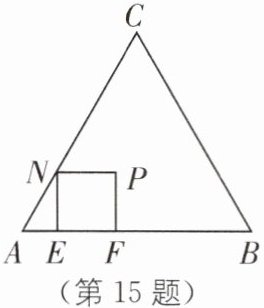
15 如图，△ABC是正三角形，正方形EFPN的顶点E，F在边AB上，顶点N在边AC上.
(1)在正三角形ABC三边及其内部，以点A为位似中心，画出正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大；(不写画法，但要保留画图痕迹)
(2)若BC = 3，求(1)中所画正方形E′F′P′N′的边长.

答案：

(1)如图，正方形E'F'P'N'即为所求. （第15题）
(2)设正方形E'F'P'N'的边长为x， 则N'P' = N'E' = E'F' = P'F' = x. 由题意，易得△CN'P'为正三角形，
∴CN' = N'P' = CP' = x.
∵正三角形ABC的边长为3，
∴AC = BC = AB = 3.
∴AN' = BP' = 3 - x.
∵在正方形E'F'P'N'中，∠N'E'F' = ∠P'F'E' = 90°，
∴∠N'E'A = ∠P'F'B = 90°.
∴AE' = BF' = $\sqrt{(3 - x)^2 - x^2}$ = $\sqrt{9 - 6x}$.
∴AB = AE' + E'F' + BF' = 2$\sqrt{9 - 6x}$ + x. 又AB = 3，
∴2$\sqrt{9 - 6x}$ + x = 3， 整理，得x² + 18x - 27 = 0， 解得x₁ = 6$\sqrt{3}$ - 9，x₂ = - 6$\sqrt{3}$ - 9(舍去).
∴正方形E'F'P'N'的边长为6$\sqrt{3}$ - 9.

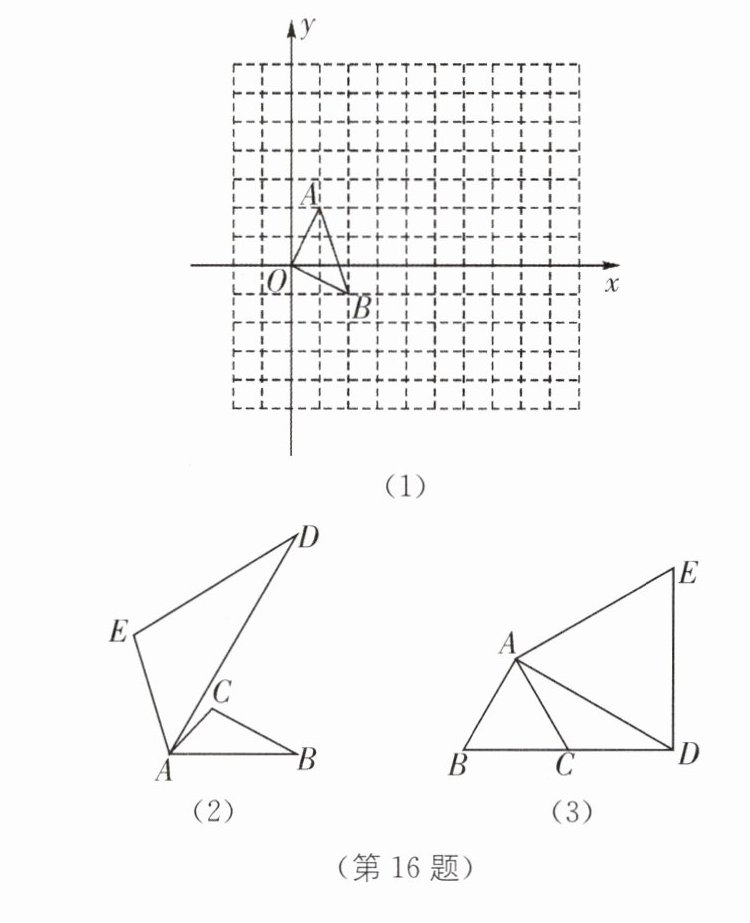
16 [开放探究性问题][问题]在正方形网格中，如图(1)，△OAB的顶点分别为O(0，0)，A(1，2)，B(2，－1).
(1)以点O(0，0)为位似中心，按比例尺3∶1在位似中心的同侧将△OAB放大为△OA′B′，放大后点A，B的对应点分别为A′，B′. 画出△OA′B′，并写出点A′，B′的坐标：A′(_______，_______)，B′(_______，_______)；
(2)在(1)中，若点C(a，b)为线段AB上任一点，写出变化后点C的对应点C′的坐标：C′(_______，_______)；
[拓展]
在平面内，先将一个多边形以点O为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为k，并且原多边形上的任一点P，它的对应点P′在线段OP或其延长线上；接着将所得多边形以点O为旋转中心，逆时针旋转一个角度θ，这种经过位似和旋转的图形变换叫做旋转相似变换，记为O(k，θ)，其中点O叫做旋转相似中心，k叫做相似比，θ叫做旋转角.
[探索]
(3)填空：如图(2)，将△ABC以点A为旋转相似中心，放大为原来的2倍，再逆时针旋转60°，得到△ADE，这个旋转相似变换记为A(_______，_______)；
(4)如图(3)，△ABC的边AB为3 cm，将它作旋转相似变换$A(\frac{4}{3},90^{\circ})$，得到△ADE，求线段BD的长.

答案：
3@@6@@6@@ - 3@@3a@@3b@@2@@60°@@
(1)如图所示，A'(3,6)，B'(6, - 3). !（第16题）
(4)
∵△ABC旋转相似变换A($\frac{4}{3}$,90°)，得到△ADE，
∴AD = $\frac{4}{3}$×3 = 4(cm)，∠BAD = 90°. 由勾股定理，得BD = $\sqrt{3^2 + 4^2}$ = 5(cm).