第79页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
11 如图,Rt△ABC 中,∠C = 90°,点 D 和点 E 分别在 BC,AB 上,若 AC = 8,CD = 2,DE⊥AB,sin B = $\frac{4}{5}$,则 ED 的长度为( ).
A. 3.2
B. 4
C. 4.5
D. 4.8

A. 3.2
B. 4
C. 4.5
D. 4.8
答案:
A
12 “健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步. 已知此步道外形近似于如图所示的 Rt△ABC,其中∠C = 90°,AB 与 BC 间另有步道 DE 相连,D 地在 AB 正中位置,E 地与 C 地相距 1 km. 若 tan∠ABC = $\frac{3}{4}$,∠DEB = 45°,小张某天沿 A→C→E→B→D→A 路线跑一圈,则他跑了________km.


答案:
24
16 如图,在平面直角坐标系中,O 为原点,四边形 ABCO 是矩形,点 A,C 的坐标分别是 A(0,2)和 C(2$\sqrt{3}$,0),点 D 是对角线 AC 上一动点(不与 A,C 点重合),连接 BD,作 DE⊥DB,交 x 轴于点 E,以线段 DE,DB 为邻边作矩形 BDEF.
(1)点 B 的坐标为________.
(2)是否存在这样的点 D,使得△DEC 是等腰三角形?若存在,请求出 AD 的长度;若不存在,请说明理由.
(3)①求证:$\frac{DE}{DB}$ = $\frac{\sqrt{3}}{3}$.
②若矩形 BDEF 的面积为 y,直接写出 y 的最小值.
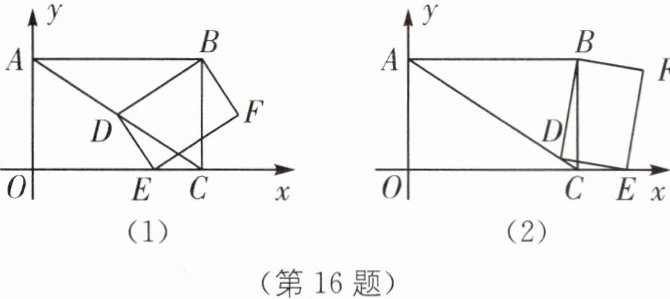
(1)点 B 的坐标为________.
(2)是否存在这样的点 D,使得△DEC 是等腰三角形?若存在,请求出 AD 的长度;若不存在,请说明理由.
(3)①求证:$\frac{DE}{DB}$ = $\frac{\sqrt{3}}{3}$.
②若矩形 BDEF 的面积为 y,直接写出 y 的最小值.

答案:
(1)$(2\sqrt{3},2)$
(2)存在。理由如下:如图
(1),连接BE,取BE的中点K,连接DK,KC。因为$\angle BDE=\angle BCE = 90^{\circ}$,所以$KD = KB = KE = KC$,所以B,D,E,C四点共圆,所以$\angle DBE=\angle DCE$,$\angle EDC=\angle EBC$。因为$\tan\angle ACO=\frac{AO}{OC}=\frac{\sqrt{3}}{3}$,所以$\angle ACO = 30^{\circ}$,$\angle ACB = 60^{\circ}$。如图
(1),当E在线段CO上时,△DEC是等腰三角形,观察图象可知,只有$ED = EC$,所以$\angle DCE=\angle EDC = 30^{\circ}$,所以$\angle BDC=\angle BCD = 60^{\circ}$,所以△DBC是等边三角形,所以$DC = BC = 2$。在Rt△AOC中,$\angle ACO = 30^{\circ}$,$OA = 2$,所以$AC = 2AO = 4$,所以$AD = AC - CD = 4 - 2 = 2$。故当$AD = 2$时,△DEC是等腰三角形。如图
(2),当E在OC的延长线上时,△DCE是等腰三角形,只有$CD = CE$,$\angle DBC=\angle DEC=\angle CDE = 15^{\circ}$,所以$\angle ABD=\angle ADB = 75^{\circ}$,所以$AB = AD = 2\sqrt{3}$。综上所述,满足条件的AD的值为2或$2\sqrt{3}$。
(3)①由
(2)可知,B,D,E,C四点共圆,所以$\angle DBE=\angle DCO = 30^{\circ}$,所以$\tan\angle DBE=\frac{DE}{DB}$,所以$\frac{DE}{DB}=\frac{\sqrt{3}}{3}$。 ②如图
(2),作$DH\perp AB$于点H。在Rt△ADH中,设$AD = x(0\lt x\lt4)$,因为$\angle DAH=\angle ACO = 30^{\circ}$,所以$DH=\frac{1}{2}AD=\frac{1}{2}x$,$AH=\sqrt{AD^{2}-DH^{2}}=\frac{\sqrt{3}}{2}x$,所以$BH = 2\sqrt{3}-\frac{\sqrt{3}}{2}x$。在Rt△BDH中,$BD=\sqrt{BH^{2}+DH^{2}}=\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$,所以$DE=\frac{\sqrt{3}}{3}BD=\frac{\sqrt{3}}{3}\cdot\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$,所以$y=\frac{\sqrt{3}}{3}[(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}]=\frac{\sqrt{3}}{3}(x^{2}-6x + 12)=\frac{\sqrt{3}}{3}(x - 3)^{2}+\sqrt{3}$。因为$0\lt x\lt4$,所以当$x = 3$时,y取最小值,y的最小值为$\sqrt{3}$。
(1)$(2\sqrt{3},2)$
(2)存在。理由如下:如图
(1),连接BE,取BE的中点K,连接DK,KC。因为$\angle BDE=\angle BCE = 90^{\circ}$,所以$KD = KB = KE = KC$,所以B,D,E,C四点共圆,所以$\angle DBE=\angle DCE$,$\angle EDC=\angle EBC$。因为$\tan\angle ACO=\frac{AO}{OC}=\frac{\sqrt{3}}{3}$,所以$\angle ACO = 30^{\circ}$,$\angle ACB = 60^{\circ}$。如图
(1),当E在线段CO上时,△DEC是等腰三角形,观察图象可知,只有$ED = EC$,所以$\angle DCE=\angle EDC = 30^{\circ}$,所以$\angle BDC=\angle BCD = 60^{\circ}$,所以△DBC是等边三角形,所以$DC = BC = 2$。在Rt△AOC中,$\angle ACO = 30^{\circ}$,$OA = 2$,所以$AC = 2AO = 4$,所以$AD = AC - CD = 4 - 2 = 2$。故当$AD = 2$时,△DEC是等腰三角形。如图
(2),当E在OC的延长线上时,△DCE是等腰三角形,只有$CD = CE$,$\angle DBC=\angle DEC=\angle CDE = 15^{\circ}$,所以$\angle ABD=\angle ADB = 75^{\circ}$,所以$AB = AD = 2\sqrt{3}$。综上所述,满足条件的AD的值为2或$2\sqrt{3}$。
(3)①由
(2)可知,B,D,E,C四点共圆,所以$\angle DBE=\angle DCO = 30^{\circ}$,所以$\tan\angle DBE=\frac{DE}{DB}$,所以$\frac{DE}{DB}=\frac{\sqrt{3}}{3}$。 ②如图
(2),作$DH\perp AB$于点H。在Rt△ADH中,设$AD = x(0\lt x\lt4)$,因为$\angle DAH=\angle ACO = 30^{\circ}$,所以$DH=\frac{1}{2}AD=\frac{1}{2}x$,$AH=\sqrt{AD^{2}-DH^{2}}=\frac{\sqrt{3}}{2}x$,所以$BH = 2\sqrt{3}-\frac{\sqrt{3}}{2}x$。在Rt△BDH中,$BD=\sqrt{BH^{2}+DH^{2}}=\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$,所以$DE=\frac{\sqrt{3}}{3}BD=\frac{\sqrt{3}}{3}\cdot\sqrt{(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}}$,所以$y=\frac{\sqrt{3}}{3}[(\frac{1}{2}x)^{2}+(2\sqrt{3}-\frac{\sqrt{3}}{2}x)^{2}]=\frac{\sqrt{3}}{3}(x^{2}-6x + 12)=\frac{\sqrt{3}}{3}(x - 3)^{2}+\sqrt{3}$。因为$0\lt x\lt4$,所以当$x = 3$时,y取最小值,y的最小值为$\sqrt{3}$。
17 阅读下列材料:
如图(1),在△ABC 中,∠A,∠B,∠C 所对的边分别为 a,b,c,可以得到:S△ABC = $\frac{1}{2}$ab sin C = $\frac{1}{2}$ac sin B = $\frac{1}{2}$bc sin A.
证明:过点 A 作 AD⊥BC,垂足为 D.
在 Rt△ABD 中,sin B = $\frac{AD}{c}$,
∴AD = c·sin B,∴S△ABC = $\frac{1}{2}$a·AD = $\frac{1}{2}$ac sin B.
同理:S△ABC = $\frac{1}{2}$ab sin C,S△ABC = $\frac{1}{2}$bc sin A.
∴S△ABC = $\frac{1}{2}$ab sin C = $\frac{1}{2}$ac sin B = $\frac{1}{2}$bc sin A.
(1)通过上述材料证明:$\frac{a}{\sin A}$ = $\frac{b}{\sin B}$ = $\frac{c}{\sin C}$;
(2)运用(1)中的结论解决问题:
如图(2),为了开发公路旁的城市荒地,测量人员选择 A,B,C 三个测量点,在 B 点测得 A 在北偏东 75°方向上,沿笔直公路向正东方向行驶 18 km 到达 C 点,测得 A 在北偏西 45°方向上,根据以上信息,求 A,B,C 三点围成的三角形的面积.(参考数据:sin 15°≈0.3,sin 120°≈0.9,$\sqrt{2}$≈1.4,结果取整数)
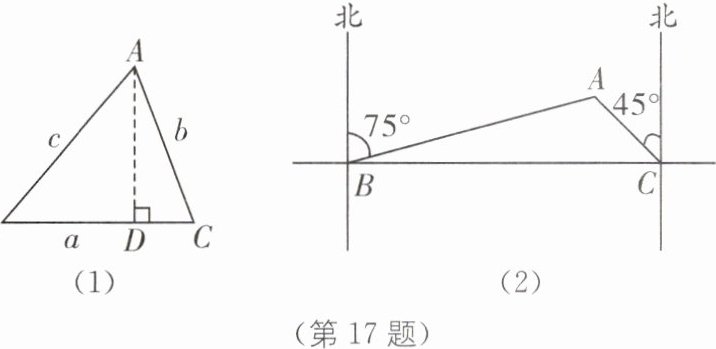
如图(1),在△ABC 中,∠A,∠B,∠C 所对的边分别为 a,b,c,可以得到:S△ABC = $\frac{1}{2}$ab sin C = $\frac{1}{2}$ac sin B = $\frac{1}{2}$bc sin A.
证明:过点 A 作 AD⊥BC,垂足为 D.
在 Rt△ABD 中,sin B = $\frac{AD}{c}$,
∴AD = c·sin B,∴S△ABC = $\frac{1}{2}$a·AD = $\frac{1}{2}$ac sin B.
同理:S△ABC = $\frac{1}{2}$ab sin C,S△ABC = $\frac{1}{2}$bc sin A.
∴S△ABC = $\frac{1}{2}$ab sin C = $\frac{1}{2}$ac sin B = $\frac{1}{2}$bc sin A.
(1)通过上述材料证明:$\frac{a}{\sin A}$ = $\frac{b}{\sin B}$ = $\frac{c}{\sin C}$;
(2)运用(1)中的结论解决问题:
如图(2),为了开发公路旁的城市荒地,测量人员选择 A,B,C 三个测量点,在 B 点测得 A 在北偏东 75°方向上,沿笔直公路向正东方向行驶 18 km 到达 C 点,测得 A 在北偏西 45°方向上,根据以上信息,求 A,B,C 三点围成的三角形的面积.(参考数据:sin 15°≈0.3,sin 120°≈0.9,$\sqrt{2}$≈1.4,结果取整数)

答案:
(1)因为$\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B$,所以$b\sin C = c\sin B$,所以$\frac{b}{\sin B}=\frac{c}{\sin C}$。同理得$\frac{a}{\sin A}=\frac{c}{\sin C}$,所以$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$。
(2)由题意,得$\angle ABC = 90^{\circ}-75^{\circ}=15^{\circ}$,$\angle ACB = 90^{\circ}-45^{\circ}=45^{\circ}$,所以$\angle A = 180^{\circ}-15^{\circ}-45^{\circ}=120^{\circ}$,由$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$,得$\frac{18}{\sin120^{\circ}}=\frac{AC}{\sin15^{\circ}}$,所以$AC\approx6\ km$,所以$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC\cdot\sin\angle ACB=\frac{1}{2}\times6\times18\times0.7\approx38(km^{2})$。故A,B,C三点围成的三角形的面积为$38\ km^{2}$。
(1)因为$\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B$,所以$b\sin C = c\sin B$,所以$\frac{b}{\sin B}=\frac{c}{\sin C}$。同理得$\frac{a}{\sin A}=\frac{c}{\sin C}$,所以$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$。
(2)由题意,得$\angle ABC = 90^{\circ}-75^{\circ}=15^{\circ}$,$\angle ACB = 90^{\circ}-45^{\circ}=45^{\circ}$,所以$\angle A = 180^{\circ}-15^{\circ}-45^{\circ}=120^{\circ}$,由$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$,得$\frac{18}{\sin120^{\circ}}=\frac{AC}{\sin15^{\circ}}$,所以$AC\approx6\ km$,所以$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC\cdot\sin\angle ACB=\frac{1}{2}\times6\times18\times0.7\approx38(km^{2})$。故A,B,C三点围成的三角形的面积为$38\ km^{2}$。
查看更多完整答案,请扫码查看


