《2025年课时训练九年级数学下册人教版江苏人民出版社》

1. （2023·西安临潼区二模）在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，已知$AC = 2$，$BC = 3$，那么下列各式中，正确的是（ ）.
A. $\sin B=\frac{2}{3}$
B. $\cos B=\frac{2}{3}$
C. $\tan B=\frac{2}{3}$
D. $\tan B=-\frac{2\sqrt{13}}{13}$

答案： **解析**：因为在Rt△ABC中，∠C = 90°，AC = 2，BC = 3，所以根据勾股定理$AB=\sqrt{2^{2}+3^{2}}=\sqrt{13}$。 - 那么$\sin B=\frac{AC}{AB}=\frac{2}{\sqrt{13}}=\frac{2\sqrt{13}}{13}$，$\cos B=\frac{BC}{AB}=\frac{3}{\sqrt{13}}=\frac{3\sqrt{13}}{13}$，$\tan B=\frac{AC}{BC}=\frac{2}{3}$。故选C。

2. 如图，在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$CD\perp AB$于点$D$，已知$\cos A=\frac{4}{5}$，则$\sin\angle DCB$的值为（ ）.

A. $\frac{9}{25}$
B. $\frac{4}{5}$
C. $\frac{3}{5}$
D. $\frac{16}{25}$

答案： **C**

3. （2023·成都新都区模拟）在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$\sin A=\frac{5}{13}$，则$\tan B =$_______.

答案：
$\frac{12}{5}$ - **解析**：如图，在Rt△ABC中，∠C = 90°，$\sin A=\frac{5}{13}=\frac{BC}{AB}$。设BC = 5a，则AB = 13a，$AC=\sqrt{AB^{2}-BC^{2}} = 12a$。 - 所以$\tan B=\frac{AC}{BC}=\frac{12a}{5a}=\frac{12}{5}$。

4. （2022·北京通州区期末）如图，在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AC = 12$，$BC = 5$. 求$\sin A$，$\cos A$和$\tan A$.

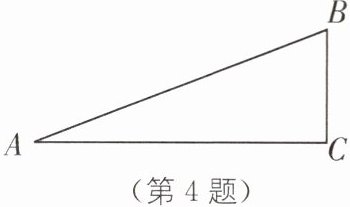
答案： 在Rt△ABC中，∠C = 90°，AC = 12，BC = 5。 - 所以$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{12^{2}+5^{2}} = 13$。 - 则$\sin A=\frac{BC}{AB}=\frac{5}{13}$，$\cos A=\frac{AC}{AB}=\frac{12}{13}$，$\tan A=\frac{BC}{AC}=\frac{5}{12}$。 - **解题关键**：本题考查锐角三角函数，掌握锐角三角函数的定义和勾股定理是正确解答的关键。

5. 计算$\sin 30^{\circ}\cdot\tan 45^{\circ}$的结果是（ ）.
A. $\frac{1}{2}$
B. $\frac{\sqrt{3}}{2}$
C. $\frac{\sqrt{3}}{6}$
D. $\frac{\sqrt{2}}{4}$

答案： **解析**：$\sin 30^{\circ}\cdot\tan 45^{\circ}=\frac{1}{2}\times1=\frac{1}{2}$。

6. 下列等式成立的是（ ）.
A. $\sin 45^{\circ}+\cos 45^{\circ}=1$
B. $2\tan 30^{\circ}=\tan 60^{\circ}$
C. $2\sin 60^{\circ}=\tan 45^{\circ}$
D. $\sin^{2}30^{\circ}=\frac{1}{2}\cos 60^{\circ}$

答案： **解析**：A. 因为$\sin 45^{\circ}+\cos 45^{\circ}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}=\sqrt{2}$，故错误，不符合题意； - B. 因为$2\tan30^{\circ}=\frac{2\sqrt{3}}{3}$，$\tan 60^{\circ}=\sqrt{3}$，所以$2\tan 30^{\circ}\neq\tan 60^{\circ}$，故错误，不符合题意； - C. 因为$2\sin 60^{\circ}=\sqrt{3}$，$\tan 45^{\circ}=1$，所以$2\sin 60^{\circ}\neq\tan 45^{\circ}$，故错误，不符合题意； - D. 因为$\sin^{2}30^{\circ}=\frac{1}{4}$，$\frac{1}{2}\cos 60^{\circ}=\frac{1}{4}$，所以$\sin^{2}30^{\circ}=\frac{1}{2}\cos 60^{\circ}$，故正确，符合题意。故选D。

7. （2023·合肥一模）若$0^{\circ}＜\alpha＜45^{\circ}$，且$\sin 2\alpha=\frac{\sqrt{3}}{2}$，则$\alpha =$_______度.

答案： **30** - **解析**：因为$\sin 2\alpha=\frac{\sqrt{3}}{2}$，$0^{\circ}＜\alpha＜45^{\circ}$，所以$2\alpha = 60^{\circ}$，所以$\alpha = 30^{\circ}$。

8. （2022·上海徐汇区模拟）计算：
- （1）$\sin^{2}60^{\circ}-\tan 30^{\circ}\cdot\cos 30^{\circ}+\tan 45^{\circ}$；
- （2）$\frac{2\sin 30^{\circ}}{2\sin 60^{\circ}-\tan 45^{\circ}}-\frac{3}{4}\cos 60^{\circ}$.

答案： -
(1)原式$=(\frac{\sqrt{3}}{2})^{2}-\frac{\sqrt{3}}{3}\times\frac{\sqrt{3}}{2}+1=\frac{3}{4}-\frac{1}{2}+1=\frac{5}{4}$。 -
(2)原式$=\frac{2\times\frac{1}{2}}{2\times\frac{\sqrt{3}}{2}-1}-\frac{3}{4}\times\frac{1}{2}=\frac{1}{\sqrt{3}-1}-\frac{3}{8}=\frac{\sqrt{3}+1}{2}-\frac{3}{8}=\frac{4\sqrt{3}+1}{8}$。

9. [情境创新类问题]某限高曲臂道路闸口如图所示，$AB$垂直地面$l_{1}$于点$A$，$BE$与水平线$l_{2}$的夹角为$\alpha(0^{\circ}\leq\alpha\leq90^{\circ})$，$EF// l_{1}// l_{2}$，若$AB = 1.4$米，$BE = 2$米，车辆的高度为$h$（单位：米），不考虑闸口与车辆的宽度：
- ①当$\alpha = 90^{\circ}$时，$h$小于$3.3$米的车辆均可以通过该闸口；
- ②当$\alpha = 45^{\circ}$时，$h$等于$2.9$米的车辆不可以通过该闸口；
- ③当$\alpha = 60^{\circ}$时，$h$等于$3.1$米的车辆不可以通过该闸口.
则上述说法正确的个数为（ ）.

A. $0$
B. $1$
C. $2$
D. $3$

答案： **解析**：由题意可得，限高曲臂道路闸口高度为$1.4 + 2\sin\alpha$。 - ①当$\alpha = 90^{\circ}$时，$h＜(1.4 + 2)$米，即$h＜3.4$米即可通过该闸口，故①正确； - ②当$\alpha = 45^{\circ}$时，$h＜(1.4 + 2\times\frac{\sqrt{2}}{2})$米，即$h＜(1.4+\sqrt{2})$即可通过该闸口。因为$2.9＞1.4+\sqrt{2}$，所以$h$等于2.9米的车辆不可以通过该闸口，故②正确； - ③当$\alpha = 60^{\circ}$时，$h＜(1.4 + 2\times\frac{\sqrt{3}}{2})$米，即$h＜(1.4+\sqrt{3})$米即可通过该闸口。因为$3.1＜1.4+\sqrt{3}$，所以$h$等于3.1米的车辆可以通过该闸口，故③不正确。故选C。