第18页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
1. (2023·株洲中考)下列哪个点在反比例函数$y = \frac{4}{x}$的图象上?( )
A. $P_1(1, - 4)$
B. $P_2(4, - 1)$
C. $P_3(2,4)$
D. $P_4(2\sqrt{2},\sqrt{2})$
A. $P_1(1, - 4)$
B. $P_2(4, - 1)$
C. $P_3(2,4)$
D. $P_4(2\sqrt{2},\sqrt{2})$
答案:
D
2. (2022·滨州中考)在同一平面直角坐标系中,函数$y = kx + 1$与$y = - \frac{k}{x}$($k$为常数且$k\neq0$)的图象大致是( )
- [此处有四个函数图象选项,依次为A、B、C、D]

- [此处有四个函数图象选项,依次为A、B、C、D]

答案:
A
3. 若反比例函数$y=(m + 1)x^{3 - m^2}$的图象在第二、四象限,则$m$的值为________.
答案:
$-2$
4. (2022·南京秦淮区二模)将函数$y = \frac{8}{x}$的图象先向左平移1个单位长度,再沿$y$轴翻折,所得到的图象对应的函数解析式是________.
答案:
$y = -\frac{8}{x - 1}$
5. 如图,已知点$A$是一次函数$y = 2x - 4$的图象与$x$轴的交点,将点$A$向上平移2个单位长度后所得的点$B$在某反比例函数图象上.
- (1)求点$A$的坐标;
- (2)确定该反比例函数的解析式.
- [此处有第5题的函数图象]
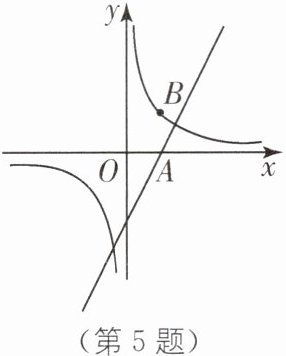
- (1)求点$A$的坐标;
- (2)确定该反比例函数的解析式.
- [此处有第5题的函数图象]

答案:
5. -
(1)因为点\(A\)是一次函数\(y = 2x - 4\)的图象与\(x\)轴的交点,所以当\(y = 0\)时,\(2x - 4 = 0\),解得\(x = 2\). 所以点\(A\)的坐标为\((2,0)\). -
(2)将点\(A(2,0)\)向上平移2个单位长度后得点\(B(2,2)\). 设过点\(B\)的反比例函数的解析式为\(y = \frac{k}{x}\),则\(2=\frac{k}{2}\),解得\(k = 4\). 所以该反比例函数的解析式为\(y = \frac{4}{x}\).
(1)因为点\(A\)是一次函数\(y = 2x - 4\)的图象与\(x\)轴的交点,所以当\(y = 0\)时,\(2x - 4 = 0\),解得\(x = 2\). 所以点\(A\)的坐标为\((2,0)\). -
(2)将点\(A(2,0)\)向上平移2个单位长度后得点\(B(2,2)\). 设过点\(B\)的反比例函数的解析式为\(y = \frac{k}{x}\),则\(2=\frac{k}{2}\),解得\(k = 4\). 所以该反比例函数的解析式为\(y = \frac{4}{x}\).
6. (2023·嘉兴中考)已知点$A( - 2,y_1)$,$B( - 1,y_2)$,$C(1,y_3)$均在反比例函数$y = \frac{3}{x}$的图象上,则$y_1$,$y_2$,$y_3$的大小关系是( ).
A. $y_1\lt y_2\lt y_3$
B. $y_2\lt y_1\lt y_3$
C. $y_3\lt y_1\lt y_2$
D. $y_3\lt y_2\lt y_1$
A. $y_1\lt y_2\lt y_3$
B. $y_2\lt y_1\lt y_3$
C. $y_3\lt y_1\lt y_2$
D. $y_3\lt y_2\lt y_1$
答案:
B
7. (2023·山西中考)若点$A( - 3,a)$,$B( - 1,b)$,$C(2,c)$都在反比例函数$y = \frac{k}{x}(k\lt0)$的图象上,则$a$,$b$,$c$的大小关系用“$\lt$”连接的结果为( ).
A. $b\lt a\lt c$
B. $c\lt b\lt a$
C. $a\lt b\lt c$
D. $c\lt a\lt b$
A. $b\lt a\lt c$
B. $c\lt b\lt a$
C. $a\lt b\lt c$
D. $c\lt a\lt b$
答案:
D
8. 已知点$A(2,m + 3)$在双曲线$y = \frac{m}{x}$上.
- (1)求此双曲线的解析式与点$A$的坐标;
- (2)如果点$B(a,5 - a)$在此双曲线上,图象经过点$A$,$B$的一次函数的函数值$y$随$x$的增大而增大,求此一次函数的解析式.
- (1)求此双曲线的解析式与点$A$的坐标;
- (2)如果点$B(a,5 - a)$在此双曲线上,图象经过点$A$,$B$的一次函数的函数值$y$随$x$的增大而增大,求此一次函数的解析式.
答案:
8. -
(1)因为点\(A(2,m + 3)\)在双曲线\(y = \frac{m}{x}\)上,所以\(m + 3=\frac{m}{2}\),解得\(m = - 6\). 所以\(m + 3 = - 3\). 所以双曲线的解析式为\(y = -\frac{6}{x}\),点\(A\)的坐标为\((2,-3)\). -
(2)因为点\(B(a,5 - a)\)在双曲线\(y = -\frac{6}{x}\)上,所以\(5 - a = -\frac{6}{a}\),解得\(a = - 1\)或\(a = 6\). 所以点\(B\)的坐标为\((-1,6)\)或\((6,-1)\). 设一次函数的解析式为\(y = kx + b\). - 当\(A(2,-3)\),\(B(-1,6)\)时,显然\(A\),\(B\)两点分别在第四、二象限,即直线\(AB\)经过第二、四象限,此时\(y\)随\(x\)的增大而减小,不符合题意,舍去; - 当\(A(2,-3)\),\(B(6,-1)\)时,将\(A\),\(B\)代入\(y = kx + b\),得\(\begin{cases}2k + b = - 3\\6k + b = - 1\end{cases}\),解得\(\begin{cases}k=\frac{1}{2}\\b = - 4\end{cases}\). 所以一次函数的解析式为\(y=\frac{1}{2}x - 4\). 因为\(\frac{1}{2}\gt0\),所以一次函数的函数值\(y\)随\(x\)的增大而增大,故一次函数的解析式为\(y=\frac{1}{2}x - 4\).
(1)因为点\(A(2,m + 3)\)在双曲线\(y = \frac{m}{x}\)上,所以\(m + 3=\frac{m}{2}\),解得\(m = - 6\). 所以\(m + 3 = - 3\). 所以双曲线的解析式为\(y = -\frac{6}{x}\),点\(A\)的坐标为\((2,-3)\). -
(2)因为点\(B(a,5 - a)\)在双曲线\(y = -\frac{6}{x}\)上,所以\(5 - a = -\frac{6}{a}\),解得\(a = - 1\)或\(a = 6\). 所以点\(B\)的坐标为\((-1,6)\)或\((6,-1)\). 设一次函数的解析式为\(y = kx + b\). - 当\(A(2,-3)\),\(B(-1,6)\)时,显然\(A\),\(B\)两点分别在第四、二象限,即直线\(AB\)经过第二、四象限,此时\(y\)随\(x\)的增大而减小,不符合题意,舍去; - 当\(A(2,-3)\),\(B(6,-1)\)时,将\(A\),\(B\)代入\(y = kx + b\),得\(\begin{cases}2k + b = - 3\\6k + b = - 1\end{cases}\),解得\(\begin{cases}k=\frac{1}{2}\\b = - 4\end{cases}\). 所以一次函数的解析式为\(y=\frac{1}{2}x - 4\). 因为\(\frac{1}{2}\gt0\),所以一次函数的函数值\(y\)随\(x\)的增大而增大,故一次函数的解析式为\(y=\frac{1}{2}x - 4\).
9. 如图,过反比例函数$y = \frac{k}{x}(x\lt0)$的图象上的一点$P$作$PQ\perp x$轴,垂足为$Q$,连接$PO$. 若$\triangle OPQ$的面积是2,则$k$的值是( ).
- A. 4
- B. - 4
- C. 2
- D. - 2
- [此处有第9题的函数图象]
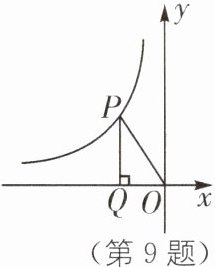
- A. 4
- B. - 4
- C. 2
- D. - 2
- [此处有第9题的函数图象]

答案:
B
查看更多完整答案,请扫码查看


