《2025年课时训练九年级数学下册人教版江苏人民出版社》

1（2023·丹东六中模拟）在△ABC中，∠C = 90°，AB = 5，BC = 4，那么∠A的正弦值是（ ）.
A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$

答案： D

2（2023·广州荔湾区一模）在Rt△ABC中，∠C = 90°，AB = 2BC，则cos A的值是（ ）.
A. $\frac{\sqrt{3}}{2}$
B. $\frac{1}{2}$
C. $\frac{2\sqrt{5}}{5}$
D. $\frac{\sqrt{5}}{5}$

答案： A

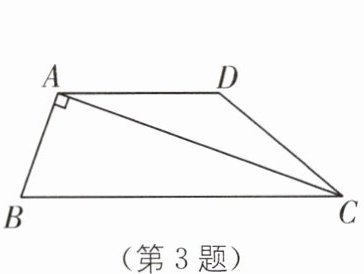
3 如图，四边形ABCD是梯形，AD//BC，CA是∠BCD的平分线，且AB⊥AC，AB = 4，AD = 6，则tan B等于（ ）.

A. 2$\sqrt{3}$
B. 2$\sqrt{2}$
C. $\frac{11}{4}$
D. $\frac{5\sqrt{5}}{4}$

答案： B

4 令a = sin 60°，b = cos 45°，c = tan 30°，则它们之间的大小关系是（ ）.
A. c＜b＜a
B. b＜c＜a
C. b＜a＜c
D. a＜c＜b

答案： A

5 在Rt△ABC中，∠ABC = 90°，AB = 3，BC = 4，则cos A的值为________.

答案： $\frac{3}{5}$

6 如图，在半径为5的⊙O中，弦AB = 6，点C是优弧$\overset{\frown}{AB}$上一点（不与A，B重合），则cos C的值为________.

答案： $\frac{4}{5}$

7 观察下列等式：
①sin 30° = $\frac{1}{2}$，cos 60° = $\frac{1}{2}$；
②sin 45° = $\frac{\sqrt{2}}{2}$，cos 45° = $\frac{\sqrt{2}}{2}$；
③sin 60° = $\frac{\sqrt{3}}{2}$，cos 30° = $\frac{\sqrt{3}}{2}$；
…
根据以上规律，计算sin²α + sin²(90° - α)=________.

答案： 1

8 如图，在等边三角形ABC中，点D是边BC上一点，延长AD到点E，使AE = AC，∠BAE的平分线交△ABC的高BF于点O，则tan∠AEO =________.

答案： $\frac{\sqrt{3}}{3}$