《2025年课时训练九年级数学下册人教版江苏人民出版社》

1 如图，在△ABC中，∠ABC为锐角，BC = 8 cm，AB = 4 cm，要在边BC上找一点D，使△ABD与△ABC相似，需要添加一个条件，以下方案不正确的是( )．

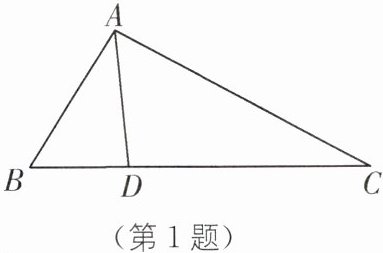
A. ∠BAD = ∠C
B. 截取CD = 6 cm
C. 使AD经过△ABC的内心
D. ∠DAC + ∠C = ∠BAC

答案： C

2 (2022·江门台山一模)如图，BD和CE是△ABC的高，则图中相似三角形共有( )．

A. 3对
B. 4对
C. 5对
D. 6对

答案： D

3 如图，如果∠BAD = ∠CAE，那么添加下列一个条件后，仍不能确定△ABC∽△ADE的是( )．

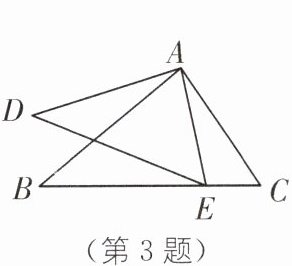
A. ∠B = ∠D
B. ∠C = ∠AED
C. $\frac{AB}{AD}=\frac{AC}{AE}$
D. $\frac{AB}{AD}=\frac{DE}{BC}$

答案： D

4 如图，点D在等边三角形ABC的边BC上，△ADE为等边三角形，DE与AC交于点F．
(1)求证：△ABD∽△DCF；
(2)除了△ABD∽△DCF外，请写出图中其他所有的相似三角形．

答案：

(1)如图. 因为△ABC，△ADE为等边三角形，所以∠B = ∠C = ∠2 = 60°。所以∠1 + ∠3 = ∠DFC + ∠3，所以∠1 = ∠DFC，所以△ABD∽△DCF。 
(2)除了△ABD∽△DCF外，图中相似三角形还有：△AEF∽△DCF，△ABD∽△AEF，△ABC∽△ADE，△ADF∽△ACD。

5 (2023·浙江宁波北仑区期中)如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED = 1，BD = 4，那么AB = _______．

答案： 4

6 如图，在Rt△ABC中，∠C = 90°，E是AC的中点，且AB = 5，AC = 4，过点E作EF⊥AB于点F，则AF = _______．

答案： $\frac{8}{5}$

7 如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．
(1)求证：△ABC∽△POA；
(2)若OB = 2，OP = $\frac{7}{2}$，求BC的长．

答案：
(1)因为BC//OP，所以∠AOP = ∠B。因为AB是直径，所以∠C = 90°。因为PA是⊙O的切线，切点为A，所以∠OAP = 90°。所以∠OAP = ∠C，所以△ABC∽△POA。
(2)因为△ABC∽△POA，所以$\frac{BC}{OA}=\frac{AB}{PO}$。因为OB = 2，PO = $\frac{7}{2}$，所以OA = 2，AB = 4。所以$\frac{BC}{2}=\frac{8}{7}$，所以BC = $\frac{16}{7}$。

8 在Rt△ABC和Rt△DEF中，∠C = ∠F = 90°，下列条件中不能判定这两个三角形相似的是( )．
A. ∠A = 55°，∠D = 35°
B. AC = 9，BC = 12，DF = 6，EF = 8
C. AC = 3，BC = 4，DF = 6，DE = 8
D. AB = 10，AC = 8，DE = 15，EF = 9

答案： C