《2025年课时训练九年级数学下册人教版江苏人民出版社》

8 (2023·西宁城西区二模)如图，从移动信号接收塔顶C处测得地面A，B两点的俯角分别为30°，45°，若该信号接收塔顶C处的高度CD为45米，点A，D，B在同一直线上，则AB两点的距离是________米. (结果精确到1米，$\sqrt{3}$≈1.73)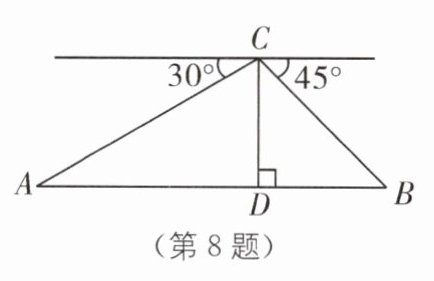

答案： 123

9 (2023·徐州中考)如图，为了测量电视塔高度，小明在云龙公园的点C处，用测角仪测得塔顶A的仰角∠AFE = 36°，他在平地上沿正对电视塔的方向后退至点D处，测得塔顶A的仰角∠AGE = 30°. 若测角仪距地面的高度FC = GD = 1.6 m，CD = 70 m，求电视塔的高度AB. (结果精确到0.1 m，参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin30° = 0.50，cos30°≈0.87，tan30°≈0.58)

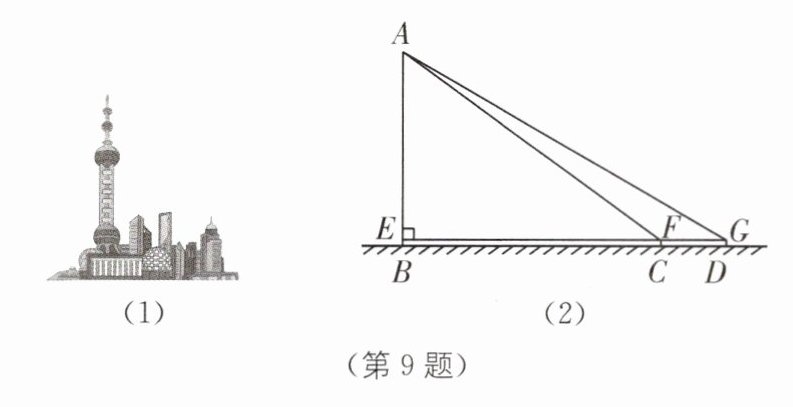
(1) (2)
(第9题)

答案： 由题意，得GE⊥AB，EB = FC = GD = 1.6 m，FG = CD = 70 m，EF = BC， 设EF = BC = x m，
∴GE = EF + FG = (x + 70)m. 在Rt△AEG中，∠AGE = 30°，
∴AE = EG·tan30°≈0.58(x + 70)m. 在Rt△AEF中，∠AFE = 36°，
∴AE = EF·tan36°≈0.73x m，
∴0.73x = 0.58(x + 70)，解得x≈270.67，
∴AE = 0.73x≈197.59 m，
∴AB = AE + BE = 197.59 + 1.6≈199.2(m)， 故电视塔的高度AB约为199.2 m.

10 [情境创新类问题](2023·孝感中考)综合实践课上，航模小组用航拍无人机进行测高实践. 如图，无人机从地面CD的中点A处竖直上升30米到达B处，测得博雅楼顶部E的俯角为45°，尚美楼顶部F的俯角为30°，已知博雅楼高度CE为15米，则尚美楼高度DF为________米. (结果保留根号)

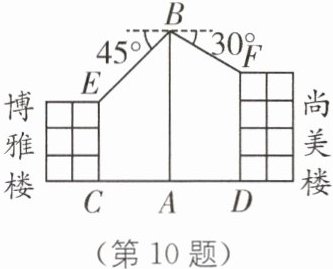
(第10题)

答案： $(30 - 5\sqrt{3})$

11 (2022·黔东南州中考)如图，校园内有一株枯死的大树AB，距树12米处有一栋教学楼CD，为了安全，学校决定砍伐该树，站在楼顶D处，测得点B的仰角为45°，点A的俯角为30°. 小青计算后得到如下结论：①AB≈18.8米；②CD≈8.4米；③若直接从点A处砍伐，树干倒向教学楼CD方向会对教学楼有影响；④若第一次在距点A的8米处的树干上砍伐，不会对教学楼CD造成危害. 其中正确的是________. (填写序号，参考数值：$\sqrt{3}$≈1.7，$\sqrt{2}$≈1.4)

(第11题)

答案： ①③④

12 (2023·长沙中考)2023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站. 如图，在发射的过程中，飞船从地面O处发射，当飞船到达A点时，从位于地面C处的雷达站测得AC的距离是8 km，仰角为30°；10 s后飞船到达B处，此时测得仰角为45°.
(1)求点A离地面的高度AO；
(2)求飞船从A处到B处的平均速度. (结果精确到0.1 km/s，参考数据：$\sqrt{3}$≈1.73)

(第12题)

答案：
(1)在Rt△AOC中，∠AOC = 90°，∠ACO = 30°，AC = 8 km，
∴$AO=\frac{1}{2}AC=\frac{1}{2}\times8 = 4$(km). 故点A离地面的高度AO为4 km.
(2)在Rt△AOC中，∠AOC = 90°，∠ACO = 30°，AC = 8 km，
∴$OC = AC\cdot\cos30^{\circ}=\frac{\sqrt{3}}{2}AC = 4\sqrt{3}$ km. 在Rt△BOC中，∠BOC = 90°，∠BCO = 45°，
∴∠BCO = ∠OBC = 45°，
∴OB = OC = $4\sqrt{3}$ km，
∴AB = OB - OA = $(4\sqrt{3}-4)$km，
∴飞船从A处到B处的平均速度=$\frac{4\sqrt{3}-4}{10}\approx0.3$(km/s).