《2025年课时训练九年级数学下册人教版江苏人民出版社》

9 (2023·天津和平区期末)如图，在△ABC中，点P在边AB上，则在下列四个条件中：①∠ACP = ∠B；②∠APC = ∠ACB；③CP·AB = AP·CB；④AC² = AP·AB，能满足△APC与△ABC相似的条件是( )．

A. ①②④
B. ①③④
C. ②③④
D. ①②③

答案： A

10 如图，在△ABC中，AB = AC，AD为BC边上的中线，DE⊥AB于点E．
(1)求证：△BDE∽△CAD；
(2)若AB = 13，BC = 10，求线段DE的长．

答案：
(1)因为AB = AC，AD为边BC上的中线，所以AD⊥BC，∠B = ∠C。因为DE⊥AB，所以∠DEB = ∠ADC = 90°，所以△BDE∽△CAD。
(2)在Rt△ADB中，AD = $\sqrt{AB^{2}-BD^{2}}=\sqrt{13^{2}-5^{2}} = 12$。因为$\frac{1}{2}AD\cdot BD=\frac{1}{2}AB\cdot DE$，所以DE = $\frac{60}{13}$。

11 如图，点E是正方形ABCD边BC上的一点(不与点B，C重合)，点F在CD边的延长线上. 连接EF交AC，AD于点G，H．
(1)请写出2对相似三角形(不添加任何辅助线)；
(2)当DF = BE时，求证：AF² = AG·AC．

答案：
(1)△CEF∽△DHF，△AHG∽△CEG，△ABC∽△ADC. (答案不唯一)
(2)连接AE。因为四边形ABCD是正方形，所以AB = AD，∠ABC = ∠ADC = ∠BCD = ∠BAD = 90°，所以∠ADF = 90° = ∠ABE。因为DF = BE，所以△ABE≌△ADF(SAS)。所以AE = AF，∠BAE = ∠DAF。所以∠EAF = ∠EAD + ∠DAF = ∠EAD + ∠BAE = 90°，所以∠AFE = 45°。因为AC是正方形ABCD的对角线，所以∠ACD = 45° = ∠AFE，所以△AFG∽△ACF。所以$\frac{AF}{AC}=\frac{AG}{AF}$，所以AF² = AG·AC。

12 如图，Rt△AB'C'是由Rt△ABC绕点A顺时针旋转得到的，连接CC'交斜边AB于点E，CC'的延长线交BB'于点F．
(1)求证：△ACE∽△FBE；
(2)设∠ABC = α，∠CAC' = β，试探索α，β满足什么关系时，△ACE与△FBE是全等三角形，并说明理由．

答案：
(1)因为Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的，所以AC = AC′，AB = AB′，∠CAB = ∠C′AB′。所以∠CAC′ = ∠BAB′，∠ACC′ = ∠AC′C，∠ABB′ = ∠AB′B。所以∠ACC′ = ∠ABB′。又∠AEC = ∠FEB，所以△ACE∽△FBE。
(2)当β = 2α时，△ACE≌△FBE。理由如下：在△ACC′中，AC = AC′，所以∠ACC′ = $\frac{180° - ∠CAC′}{2}=\frac{180° - β}{2}=90° - α$。在Rt△ABC中，∠ACC′ + ∠BCE = 90°，即90° - α + ∠BCE = 90°，所以∠BCE = α。因为∠ABC = α，所以∠ABC = ∠BCE，所以CE = BE。由
(1)，∠ACC′∽∠ABB′，∠AEC = ∠FEB，所以△ACE≌△FBE(ASA)。

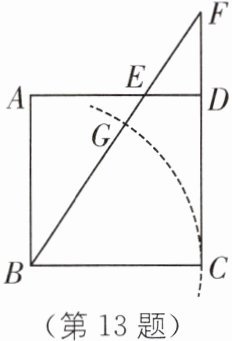
13 (2023·杭州中考)如图，在边长为1的正方形ABCD中，点E在边AD上(不与点A，D重合)，射线BE与射线CD交于点F．
(1)若ED = $\frac{1}{3}$，求DF的长；
(2)求证：AE·CF = 1；
(3)以点B为圆心，BC长为半径画弧，交线段BE于点G．若EG = ED，求ED的长．

答案：
(1)因为ED = $\frac{1}{3}$，所以AE = $\frac{2}{3}$。由题意，得AB//FC，所以△ABE∽△DFE，所以$\frac{AB}{DF}=\frac{AE}{DE}=2$。因为AB = 1，所以DF = $\frac{1}{2}$。
(2)由题意，得AD//BC，所以∠AEB = ∠CBF。又因为∠A = ∠C，所以△ABE∽△CFB，所以$\frac{AE}{CB}=\frac{AB}{CF}$。因为AB = BC = 1，所以AE·CF = AB·BC = 1。
(3)设EG = ED = x，则AE = 1 - x，BE = 1 + x。在Rt△ABE中，由勾股定理，得(1 - x)² + 1² = (1 + x)²，解得x = $\frac{1}{4}$，所以ED的长为$\frac{1}{4}$。