《2025年课时训练九年级数学下册人教版江苏人民出版社》

1 在 Rt△ABC 中，∠C = 90°，a，b，c 分别为∠A，∠B，∠C 的对边，则下列各式中能成立的是( )．
A. b = c cos B
B. c = b sin B
C. tan B = $\frac{b}{a}$
D. tan A = $\frac{b}{a}$

答案： C

2（2023·哈尔滨道外区三模）在 Rt△ABC 中，∠C = 90°，∠B = 50°，AB = 9，则 BC 的长为( )．
A. 9 sin 50°
B. 9 cos 50°
C. 9 tan 40°
D. 9 cos 40°

答案： B

3 如图，在△ABC 中，AC = 2，∠B = 45°，∠C = 30°，则 BC 的长度为( )．

A. $\sqrt{3}$
B. 2
C. 1 + $\sqrt{3}$
D. 3

答案： C

4（2023·常州外国语学校一模）在锐角三角形 ABC 中，sin A = $\frac{3\sqrt{10}}{10}$，cos B = $\frac{4}{5}$，若 AB = 15，则 AC = ________．

答案： $3\sqrt{10}$

5 在△ABC 中，AD⊥BC 于 D，若 tan∠CAD = $\frac{1}{2}$，AB = 5，AD = 3，则 BC = ________．

答案： 5.5或2.5

6 如图，某校自行车棚的人字架棚顶为等腰三角形，D 是 AB 的中点，中柱 CD = 1 m，∠A = 27°，则跨度 AB 的长为________m.（精确到 0.01 m）

答案： 3.93

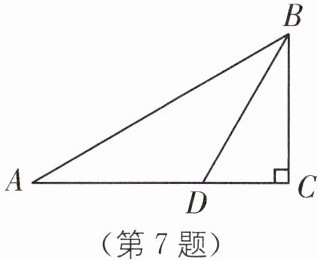
7 如图，在 Rt△ABC 中，∠C = 90°，∠A = 30°，BD 是∠ABC 的平分线，CD = 5 cm，求 AB 的长.

答案： 因为在Rt△ABC中，$\angle C = 90^{\circ}$，$\angle A = 30^{\circ}$，BD是$\angle ABC$的平分线，所以$\angle ABD=\angle CBD = 30^{\circ}$，所以$AD = DB$。在Rt△CBD中，$CD = 5\ cm$，所以$BC = 5\sqrt{3}\ cm$，则$AB = 2BC = 10\sqrt{3}\ cm$。

8 在 Rt△ABC 中，∠C = 90°，a = 4$\sqrt{6}$，b = 12$\sqrt{2}$，求∠A，∠B 和 c．

答案： 因为$\tan A=\frac{BC}{AC}=\frac{4\sqrt{6}}{12\sqrt{2}}=\frac{\sqrt{3}}{3}$，所以$\angle A = 30^{\circ}$。因为$\tan B=\frac{AC}{BC}=\frac{12\sqrt{2}}{4\sqrt{6}}=\sqrt{3}$，所以$\angle B = 60^{\circ}$。因为$\angle C = 90^{\circ}$，所以$c^{2}=a^{2}+b^{2}$，所以$c=\sqrt{(4\sqrt{6})^{2}+(12\sqrt{2})^{2}} = 8\sqrt{6}$。

9（2023·西安雁塔一中四模）如图，在△ABC 中，AB = 6，∠A = 45°，∠B = 75°，求 AB 边上的高.

答案： 过点B作$BD\perp AC$于D，则$\angle BDA=\angle BDC = 90^{\circ}$，因为$\angle A = 45^{\circ}$，所以$\angle ABD = 45^{\circ}=\angle A$，所以$AD = BD$。因为$AB = 6$，所以$BD = AD = AB\cdot\sin A = 6\times\frac{\sqrt{2}}{2}=3\sqrt{2}$。因为$\angle ABC = 75^{\circ}$，$\angle ABD = 45^{\circ}$，所以$\angle CBD = 30^{\circ}$。在Rt△BDC中，$\tan30^{\circ}=\frac{CD}{BD}$，所以$CD = BD\cdot\tan30^{\circ}=3\sqrt{2}\times\frac{\sqrt{3}}{3}=\sqrt{6}$，所以$AC = AD + CD = 3\sqrt{2}+\sqrt{6}$。设AB边上的高为h，因为$S_{\triangle ACB}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\times(3\sqrt{2}+\sqrt{6})\times3\sqrt{2}=9 + 3\sqrt{3}$，所以$\frac{1}{2}AB\cdot h = 9 + 3\sqrt{3}$，解得$h = 3+\sqrt{3}$，即AB边上的高为$3+\sqrt{3}$。