第31页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
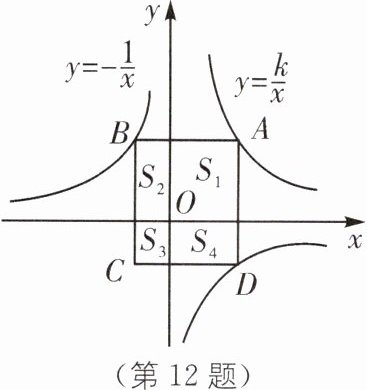
12(2023·广西中考)如图,过$y = \frac{k}{x}$($x>0$)的图象上点$A$,分别作$x$轴,$y$轴的平行线交$y = - \frac{1}{x}$的图象于$B$,$D$两点,以$AB$,$AD$为邻边的矩形$ABCD$被坐标轴分割成四个小矩形,面积分别记为$S_1$,$S_2$,$S_3$,$S_4$,若$S_2 + S_3 + S_4 = \frac{5}{2}$,则$k$的值为( ).
A. 4
B. 3
C. 2
D. 1

A. 4
B. 3
C. 2
D. 1
答案:
C
13(2023·兰州中考)如图,反比例函数$y = \frac{k}{x}$($x<0$)与一次函数$y = -2x + m$的图象交于点$A(-1,4)$,$BC \perp y$轴于点$D$,分别交反比例函数与一次函数的图象于点$B$,$C$.
(1)求反比例函数$y = \frac{k}{x}$与一次函数$y = -2x + m$的解析式;
(2)当$OD = 1$时,求线段$BC$的长.

(1)求反比例函数$y = \frac{k}{x}$与一次函数$y = -2x + m$的解析式;
(2)当$OD = 1$时,求线段$BC$的长.

答案:
13. - (1)因为反比例函数$y = \frac{k}{x}(x < 0)$与一次函数$y = -2x + m$的图象交于点$A(-1,4)$,所以$4 = \frac{k}{-1}$,$4 = -2×(-1)+m$,所以$k = -4$,$m = 2$,所以反比例函数的解析式为$y = -\frac{4}{x}$,一次函数的解析式为$y = -2x + 2$。 - (2)因为$BC⊥y$轴于点$D$,所以$BC∥x$轴。因为$OD = 1$,所以$B$,$C$的纵坐标为$1$,所以$B(-4,1)$,$C(\frac{1}{2},1)$,所以$BC = \frac{1}{2}+4 = 4\frac{1}{2}$。
14 [跨学科综合](2023·吉林中考)笑笑同学通过学习数学和物理知识,知道了电磁波的波长$\lambda$(单位:m)会随着电磁波的频率$f$(单位:MHz)的变化而变化.已知波长$\lambda$与频率$f$是反比例函数关系,下面是它们的部分对应值:
|频率$f$/MHz|10|15|50|
|----|----|----|----|
|波长$\lambda$/m|30|20|6|
(1)求波长$\lambda$关于频率$f$的函数解析式;
(2)当$f = 75$MHz时,求此电磁波的波长$\lambda$.
|频率$f$/MHz|10|15|50|
|----|----|----|----|
|波长$\lambda$/m|30|20|6|
(1)求波长$\lambda$关于频率$f$的函数解析式;
(2)当$f = 75$MHz时,求此电磁波的波长$\lambda$.
答案:
14. - (1)设波长$\lambda$关于频率$f$的函数解析式为$\lambda = \frac{k}{f}(k≠0)$,把点$(10,30)$代入上式中,得$\frac{k}{10}=30$,解得$k = 300$,所以波长$\lambda$关于频率$f$的函数解析式为$\lambda = \frac{300}{f}$。 - (2)当$f = 75MHz$时,$\lambda = \frac{300}{75}=4(m)$。故当$f = 75MHz$时,此电磁波的波长$\lambda$为$4m$。
15 已知某电路的电压$U$(V),电流$I$(A),电阻$R$($\Omega$)三者之间有关系式$U = IR$,且电路的电压$U$恒为220 V.
(1)求出电流$I$关于电阻$R$的函数表达式;
(2)若该电路的电阻为250 $\Omega$,则通过它的电流是多少?
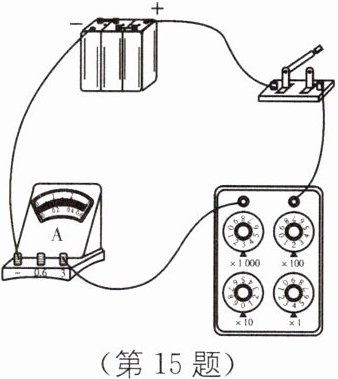
(3)如图,怎样调整电阻箱$R$的值,可以使电路中的电流$I$增大? 若电流$I = 1.1$ A,求电阻$R$的值.
(1)求出电流$I$关于电阻$R$的函数表达式;
(2)若该电路的电阻为250 $\Omega$,则通过它的电流是多少?
(3)如图,怎样调整电阻箱$R$的值,可以使电路中的电流$I$增大? 若电流$I = 1.1$ A,求电阻$R$的值.

答案:
15. - (1)因为某电路的电压$U(V)$,电流$I(A)$,电阻$R(\Omega)$三者之间有解析式$U = IR$,所以$I = \frac{U}{R}$。将$U = 220$代入,得$I = \frac{220}{R}$,所以电流$I$关于电阻$R$的函数解析式是$I = \frac{220}{R}$。 - (2)当$R = 250\Omega$时,$I = \frac{220}{250}=0.88(A)$,所以若该电路的电阻为$250\Omega$,则通过它的电流是$0.88A$。 - (3)因为$I = \frac{220}{R}$,所以电流$I$与电阻$R$成反比例关系。所以要使电路中的电流$I$增大,可以减少电阻$R$。当$I = 1.1A$时,$\frac{220}{R}=1.1$,解得$R = 200$。故若电流$I = 1.1A$,则电阻$R$的值为$200\Omega$。
查看更多完整答案,请扫码查看


