第46页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
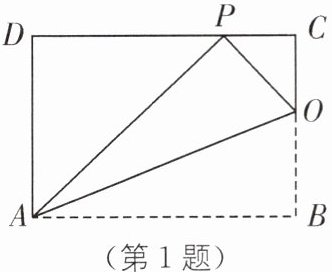
1 已知矩形ABCD的一条边AD = 8,将矩形ABCD折叠,使得顶点B落在边CD上的点P处,折痕与边BC交于点O,连接AP,OP,OA.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4.
①求边CP的长;
②求边AB的长.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4.
①求边CP的长;
②求边AB的长.

答案:
(1)因为四边形ABCD是矩形,
所以AD = BC,DC = AB,∠B = ∠C = ∠D = 90°。
由折叠可得AP = AB,PO = BO,∠PAO = ∠BAO,∠APO = ∠B。所以∠APO = 90°。
所以∠APD = 90° - ∠CPO = ∠POC。
因为∠D = ∠C,∠APD = ∠POC,所以△OCP∽△PDA。
(2)①因为△OCP与△PDA的面积比为1∶4,
所以$\frac{OC}{PD}=\frac{OP}{PA}=\frac{CP}{DA}=\sqrt{\frac{1}{4}}=\frac{1}{2}$。
所以PD = 2OC,PA = 2OP,DA = 2CP。
因为AD = 8,所以CP = 4。
②设OP = x,则OB = x,CO = 8 - x。
在Rt△PCO中,
∠C = 90°,CP = 4,OP = x,CO = 8 - x,
所以$x^{2}=(8 - x)^{2}+4^{2}$,解得x = 5。
所以AB = AP = 2OP = 10。故边AB的长为10。
2 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB = 2,BC = 3,请直接写出所有满足条件的AC的长;
(2)如图(1),在四边形ABCD中,AD//BC,对角线BD平分∠ABC,∠BAC = ∠ADC.
①求证:△ABC∽△DCA;
②求证:△ABC是比例三角形.
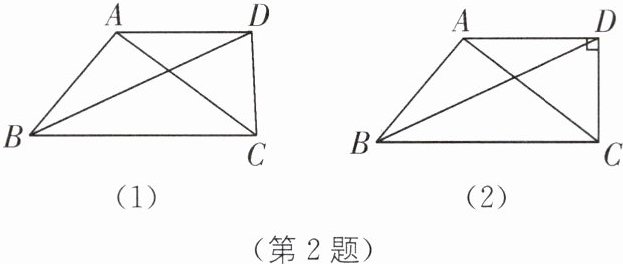
(3)如图(2),在(2)的条件下,当∠ADC = 90°时,求出$\frac{BD}{AC}$的值.
(1)已知△ABC是比例三角形,AB = 2,BC = 3,请直接写出所有满足条件的AC的长;
(2)如图(1),在四边形ABCD中,AD//BC,对角线BD平分∠ABC,∠BAC = ∠ADC.
①求证:△ABC∽△DCA;
②求证:△ABC是比例三角形.

(3)如图(2),在(2)的条件下,当∠ADC = 90°时,求出$\frac{BD}{AC}$的值.
答案:
(1)由△ABC是比例三角形,且AB = 2,BC = 3, ①当$AB^{2}=BC\cdot AC$时,得4 = 3AC,解得$AC=\frac{4}{3}$; ②当$BC^{2}=AB\cdot AC$时,得9 = 2AC,解得$AC=\frac{9}{2}$; ③当$AC^{2}=AB\cdot BC$时,得$AC^{2}=6$,解得$AC = \sqrt{6}$(负值舍去)。 所以当$AC=\frac{4}{3}$或$\frac{9}{2}$或$\sqrt{6}$时,△ABC是比例三角形。 (2)①因为AD//BC,所以∠ACB = ∠CAD。 又∠BAC = ∠ADC,所以△ABC∽△DCA。 ②由①知,△ABC∽△DCA, 所以$\frac{BC}{AC}=\frac{AC}{AD}$,即$AC^{2}=BC\cdot AD$。 因为AD//BC,所以∠ADB = ∠CBD。 因为BD平分∠ABC,所以∠ABD = ∠CBD, 所以∠ADB = ∠ABD,所以AB = AD, 所以$AC^{2}=BC\cdot AB$,所以△ABC是比例三角形。(3)如图,过点A作AH⊥BD于点H。 因为AB = AD,所以$BH=\frac{1}{2}BD$。 因为AD//BC,∠ADC = 90°,所以∠BCD = 90°, 所以∠BHA = ∠BCD = 90°。 又∠ABH = ∠DBC,所以△ABH∽△DBC, 所以$\frac{AB}{DB}=\frac{BH}{BC}$,即AB·BC = BH·DB, 所以$AB\cdot BC=\frac{1}{2}BD^{2}$。又AB·BC = AC², 所以$\frac{1}{2}BD^{2}=AC^{2}$,所以$\frac{BD}{AC}=\sqrt{2}$(负值舍去)。
因为AB = AD,所以$BH=\frac{1}{2}BD$。 因为AD//BC,∠ADC = 90°,所以∠BCD = 90°, 所以∠BHA = ∠BCD = 90°。 又∠ABH = ∠DBC,所以△ABH∽△DBC, 所以$\frac{AB}{DB}=\frac{BH}{BC}$,即AB·BC = BH·DB, 所以$AB\cdot BC=\frac{1}{2}BD^{2}$。又AB·BC = AC², 所以$\frac{1}{2}BD^{2}=AC^{2}$,所以$\frac{BD}{AC}=\sqrt{2}$(负值舍去)。
(1)由△ABC是比例三角形,且AB = 2,BC = 3, ①当$AB^{2}=BC\cdot AC$时,得4 = 3AC,解得$AC=\frac{4}{3}$; ②当$BC^{2}=AB\cdot AC$时,得9 = 2AC,解得$AC=\frac{9}{2}$; ③当$AC^{2}=AB\cdot BC$时,得$AC^{2}=6$,解得$AC = \sqrt{6}$(负值舍去)。 所以当$AC=\frac{4}{3}$或$\frac{9}{2}$或$\sqrt{6}$时,△ABC是比例三角形。 (2)①因为AD//BC,所以∠ACB = ∠CAD。 又∠BAC = ∠ADC,所以△ABC∽△DCA。 ②由①知,△ABC∽△DCA, 所以$\frac{BC}{AC}=\frac{AC}{AD}$,即$AC^{2}=BC\cdot AD$。 因为AD//BC,所以∠ADB = ∠CBD。 因为BD平分∠ABC,所以∠ABD = ∠CBD, 所以∠ADB = ∠ABD,所以AB = AD, 所以$AC^{2}=BC\cdot AB$,所以△ABC是比例三角形。(3)如图,过点A作AH⊥BD于点H。
 因为AB = AD,所以$BH=\frac{1}{2}BD$。 因为AD//BC,∠ADC = 90°,所以∠BCD = 90°, 所以∠BHA = ∠BCD = 90°。 又∠ABH = ∠DBC,所以△ABH∽△DBC, 所以$\frac{AB}{DB}=\frac{BH}{BC}$,即AB·BC = BH·DB, 所以$AB\cdot BC=\frac{1}{2}BD^{2}$。又AB·BC = AC², 所以$\frac{1}{2}BD^{2}=AC^{2}$,所以$\frac{BD}{AC}=\sqrt{2}$(负值舍去)。
因为AB = AD,所以$BH=\frac{1}{2}BD$。 因为AD//BC,∠ADC = 90°,所以∠BCD = 90°, 所以∠BHA = ∠BCD = 90°。 又∠ABH = ∠DBC,所以△ABH∽△DBC, 所以$\frac{AB}{DB}=\frac{BH}{BC}$,即AB·BC = BH·DB, 所以$AB\cdot BC=\frac{1}{2}BD^{2}$。又AB·BC = AC², 所以$\frac{1}{2}BD^{2}=AC^{2}$,所以$\frac{BD}{AC}=\sqrt{2}$(负值舍去)。 3 (2023·昭通昭阳区二模)如图(1),四边形ABCD是正方形,点E是对角线AC上一点(点E不与点A,C重合),过点E作EF//CD,交BC于点F,作EG//BC,交CD于点G.
(1)求证:四边形EFCG是正方形;
(2)如图(2),将四边形EFCG绕点C顺时针旋转α(0°<α<90°),连接AE,DG,求$\frac{AE}{DG}$的值.

(1)求证:四边形EFCG是正方形;
(2)如图(2),将四边形EFCG绕点C顺时针旋转α(0°<α<90°),连接AE,DG,求$\frac{AE}{DG}$的值.

答案:
(1)因为四边形ABCD是正方形,
所以∠BCD = 90°,∠ACB = ∠ACD = 45°。
因为EG//BC,EF//CD,
所以四边形EFCG是平行四边形。
因为∠FCG = 90°,所以平行四边形EFCG是矩形,
所以EF⊥BC,EG⊥CD,
所以EF = EG(角平分线的性质),
所以矩形EFCG是正方形。
(2)因为四边形ABCD,EFCG都是正方形,
所以$\frac{AC}{CD}=\frac{CE}{CG}=\sqrt{2}$,∠ACD = ∠ECG = 45°,
所以∠ACE = ∠DCG,所以△ACE∽△DCG,
所以$\frac{AE}{DG}=\frac{AC}{CD}=\sqrt{2}$。
查看更多完整答案,请扫码查看


