《2025年课时训练九年级数学下册人教版江苏人民出版社》

8. (2023·哈尔滨南岗区十七中四模)如图，小明设计的用激光笔测量城墙高度的示意图，在点 $P$ 处水平放置一面平面镜，光线从点 $A$ 出发经平面镜反射后刚好射到城墙 $CD$ 的顶端 $C$ 处，已知 $AB\perp BD$，$CD\perp BD$，$AB = 1.2$ 米，$BP = 1.8$ 米，$PD = 12$ 米，那么该城墙 $CD$ 的高度为（ ）.

A. $6$ 米
B. $8$ 米
C. $10$ 米
D. $18$ 米

答案： B

9. (2023·石家庄裕华区二模)如图，某同学在 $A$ 处看见河对岸有一大树 $P$，想测得 $A$ 与 $P$ 的距离. 他先从 $A$ 向正西走 $90\ m$ 到达 $P$ 的正南方 $C$ 处，再回到 $A$ 向正南走 $30\ m$ 到 $D$ 处，再从 $D$ 处向正东走到 $E$ 处，使得 $E$，$A$，$P$ 三点恰好在一条直线上，测得 $DE = 22.5\ m$，则 $A$ 与 $P$ 的距离为（ ）.

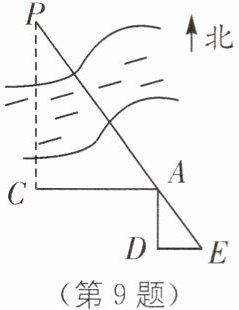
A. $112.5\ m$
B. $120\ m$
C. $135\ m$
D. $150\ m$

答案： D

10. 学校门口的栏杆如图所示，栏杆从水平位置 $BD$ 绕 $O$ 点旋转到 $AC$ 位置，已知 $AB\perp BD$，$CD\perp BD$，垂足分别为 $B$，$D$，$AO = 4\ m$，$AB = 1.6\ m$，$CO = 1\ m$，则栏杆 $C$ 端应下降的垂直距离 $CD$ 为（ ）.

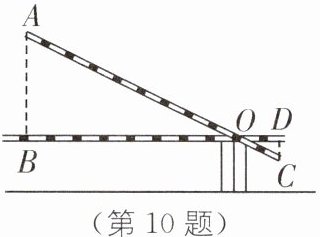
A. $0.2\ m$
B. $0.3\ m$
C. $0.4\ m$
D. $0.5\ m$

答案： C

11. [情境创新类问题](2022·广西中考)古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔影子的顶部直立一根木杆，借助太阳光测金字塔的高度. 如图，木杆 $EF$ 长 $2$ 米，它的影长 $FD$ 是 $4$ 米，同一时刻测得 $OA$ 是 $268$ 米，则金字塔的高度 $BO$ 是_______米.

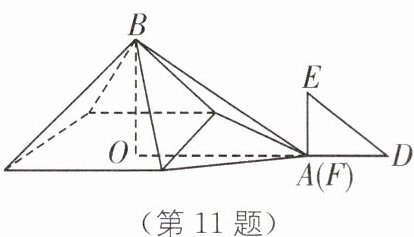
答案： 134

12. [情境创新类问题](2023·西安莲湖区模拟)为测量一棵大树的高度，设计的测量方案如图所示：标杆高度 $CD = 3\ m$，人的眼睛 $A$、标杆的顶端 $C$ 和大树顶端 $M$ 在一条直线上，标杆与大树的水平距离 $DN = 14\ m$，人的眼睛与地面的高度 $AB = 1.6\ m$，人与标杆 $CD$ 的水平距离 $BD = 2\ m$，$B$，$D$，$N$ 三点共线，$AB\perp BN$，$CD\perp BN$，$MN\perp BN$，求大树 $MN$ 的高度.

答案：
如图所示，过点A作AF⊥MN于点F，交CD于点E。依题意，得B，D，N三点共线，AB⊥BN，CD⊥BN，MN⊥BN， 所以四边形ABDE，ABNF是矩形， 所以AE = BD = 2 m，CE = CD - AB = 3 - 1.6 = 1.4（m），AF = BN = BD + DN = 2 + 14 = 16（m），FN = AB = 1.6 m。 因为CD⊥BN，MN⊥BN， 所以CE//MF，所以△ACE∽△AMF， 所以$\frac{CE}{MF}=\frac{AE}{AF}$，即$\frac{1.4}{MF}=\frac{2}{16}$，解得MF = 11.2 m， 所以MN = MF + FN = 11.2 + 1.6 = 12.8（m）， 故大树MN的高度为12.8 m。

13. (2023·西安灞桥区模拟)如图，为了估算河面的宽度，即 $EP$ 的长，在离河岸 $D$ 点 $2$ 米远的 $B$ 点，立一根长为 $1$ 米的标杆 $AB$，在河对岸的岸边有一块高为 $2.5$ 米的安全警示牌 $MF$，警示牌的顶端 $M$ 在河里的倒影为点 $N$，即 $PM = PN$，两岸均高出水平面 $1.25$ 米，即 $DE = FP = 1.25$ 米，经测量此时 $A$，$D$，$N$ 三点在同一直线上，并且点 $M$，$F$，$P$，$N$ 共线，点 $B$，$D$，$F$ 共线，若 $AB$，$DE$，$MF$ 均垂直于河面 $EP$，求河宽 $EP$ 是多少米.

答案：
如图，设AN交EP于点O，延长AB交EP的反向延长线于点H， 则四边形BDEH是矩形， 所以BH = DE = 1.25米，HE = BD = 2米，BD//EH， 所以AH = AB + BH = 1 + 1.25 = 2.25（米）。 因为BD//OH，所以△ABD∽△AHO， 所以$\frac{BD}{HO}=\frac{AB}{AH}$，即$\frac{2}{OH}=\frac{1}{2.25}$，所以HO = 4.5米，OE = OH - HE = 4.5 - 2 = 2.5（米）。 因为MF = 2.5米，FP = 1.25米， 所以PN = PM = MF + FP = 3.75米。 因为AH⊥EP，PN⊥EP， 所以AH//PN，所以△AHO∽△NPO， 所以$\frac{AH}{NP}=\frac{HO}{PO}$，即$\frac{2.25}{3.75}=\frac{4.5}{PO}$，所以PO = 7.5米， 所以PE = PO + OE = 7.5 + 2.5 = 10（米）。 故河宽EP是10米。