《2025年课时训练九年级数学下册人教版江苏人民出版社》

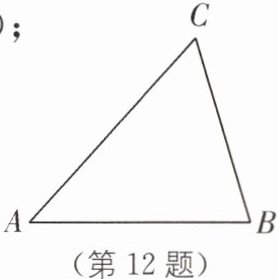
12. 如图，在$\triangle ABC$中，$AB = 8$，$AC = 9$，$\angle A = 48^{\circ}$。求：
（1）$AB$边上的高（精确到0.01）；
（2）$\angle B$的度数（精确到$1'$）。

答案：

(1)如图，作AB边上的高CH，垂足为H。在Rt△ACH中，$\sin A=\frac{CH}{AC}$，
∴$CH = AC\cdot\sin A=9\sin48^{\circ}\approx6.69$。
(2)在Rt△ACH中，$\cos A=\frac{AH}{AC}$，
∴$AH = AC\cdot\cos A=9\cos48^{\circ}$。 在Rt△BCH中， $\tan B=\frac{CH}{BH}=\frac{CH}{AB - AH}=\frac{9\sin48^{\circ}}{8 - 9\cos48^{\circ}}\approx3.382$，
∴$∠B\approx73^{\circ}32'$。

13. 已知三角函数值，可以先利用计算器求出锐角$\alpha$与$\beta$，从而比较它们的大小。你能否不用计算器来比较以下的锐角$\alpha$与$\beta$的大小？如果能，说说你的想法。
（1）$\cos\alpha=\frac{3}{4}$，$\tan\beta=\frac{5}{4}$；
（2）$\sin\alpha = 0.4567$，$\cos\beta = 0.5678$。

答案：
(1)$\cos\alpha=\frac{3}{4}$，$\alpha\approx41.41^{\circ}$，$\tan\beta=\frac{5}{4}$，$\beta\approx51.34^{\circ}$，
∴$\alpha＜\beta$。 可以不用计算器来比较锐角$\alpha$的大小。
∵$\cos\alpha=\frac{3}{4}＞\frac{\sqrt{2}}{2}=\cos45^{\circ}$，
∴$\alpha＜45^{\circ}$。
∵$\tan\beta=\frac{5}{4}＞1=\tan45^{\circ}$，
∴$\beta＞45^{\circ}$。
∴$\alpha＜\beta$。
(2)$\sin\alpha = 0.4567$，$\alpha\approx27.17^{\circ}$，$\cos\beta = 0.5678$，$\beta\approx55.40^{\circ}$，
∴$\alpha＜\beta$。
∵$\sin\alpha=0.4567＜\frac{1}{2}=\sin30^{\circ}$，
∴$\alpha＜30^{\circ}$。
∵$\cos\beta=0.5678＜\frac{\sqrt{2}}{2}=\cos45^{\circ}$，
∴$\beta＞45^{\circ}$
∴$\alpha＜\beta$。

14. 已知三角函数值，用计算器求锐角$A$和$B$，并从中总结规律：
（1）$\sin A = 0.3547$，$\cos B = 0.3547$；
（2）$\sin A = 0.65$，$\cos B = 0.65$。

答案：
(1)由$\sin A = 0.3547$，可得$∠A\approx20.78^{\circ}$， 由$\cos B = 0.3547$，可得$∠B\approx69.22^{\circ}$， 由此可得，$∠A + ∠B = 90^{\circ}$。
(2)由$\sin A = 0.65$，可得$∠A\approx40.54^{\circ}$， 由$\cos B = 0.65$，可得$∠B\approx49.46^{\circ}$， 由此可得，$∠A + ∠B = 90^{\circ}$。

15.（1）验证下列两组数值的关系：
$2\sin30^{\circ}\cdot\cos30^{\circ}$与$\sin60^{\circ}$；
$2\sin22.5^{\circ}\cdot\cos22.5^{\circ}$与$\sin45^{\circ}$。
（2）用一句话概括上面的关系。
（3）试一试：你自己任选一个锐角，用计算器验证上述结论是否成立。
（4）如果结论成立，试用$\alpha$表示一个锐角，写出这个解析式。

答案：
(1)
∵$2\sin30^{\circ}\cdot\cos30^{\circ}=2\times\frac{1}{2}\times\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$，$\sin60^{\circ}=\frac{\sqrt{3}}{2}$，$2\sin22.5^{\circ}\cdot\cos22.5^{\circ}\approx2\times0.38\times0.92\approx0.7$， $\sin45^{\circ}=\frac{\sqrt{2}}{2}\approx0.7$，
∴$2\sin30^{\circ}\cdot\cos30^{\circ}=\sin60^{\circ}$，$2\sin22.5^{\circ}\cdot\cos22.5^{\circ}=\sin45^{\circ}$。
(2)由
(1)可知，一个角正弦与余弦积的2倍，等于该角2倍的正弦值。
(3)$2\sin15^{\circ}\cdot\cos15^{\circ}\approx2\times0.26\times0.97\approx\frac{1}{2}$，$\sin30^{\circ}=\frac{1}{2}$。(答案不唯一)
(4)$2\sin\alpha\cdot\cos\alpha=\sin2\alpha$。

16.（1）先用计算器求下列正弦值（精确到0.0001），然后用“＜”把它们连接起来。
$\sin8^{\circ}$，$\sin55^{\circ}7'$，$\sin89^{\circ}13'$，$\sin22^{\circ}43'20''$。
（2）先用计算器求下列余弦值（精确到0.0001），然后用“＜”把它们连接起来。
$\cos10^{\circ}$，$\cos78^{\circ}40'$，$\cos45^{\circ}$，$\cos40^{\circ}8'54''$。
（3）由（1），（2）你能得到什么结论？

答案：
(1)
∵$\sin8^{\circ}\approx0.1392$，$\sin55^{\circ}7'\approx0.8203$，$\sin89^{\circ}13'\approx0.9999$，$\sin22^{\circ}43'20''\approx0.3863$，
∴$\sin8^{\circ}＜\sin22^{\circ}43'20''＜\sin55^{\circ}7'＜\sin89^{\circ}13'$。
(2)
∵$\cos10^{\circ}\approx0.9848$，$\cos78^{\circ}40'\approx0.1965$，$\cos45^{\circ}\approx0.7071$，$\cos40^{\circ}8'54''\approx0.7644$，
∴$\cos78^{\circ}40'＜\cos45^{\circ}＜\cos40^{\circ}8'54''＜\cos10^{\circ}$。
(3)结论：锐角函数的正弦值随角度的增加而增加，锐角函数的余弦值随角度的增加而减小。

17.（1）用计算器计算并验证$\sin25^{\circ}+\sin46^{\circ}$与$\sin71^{\circ}$之间的大小关系；
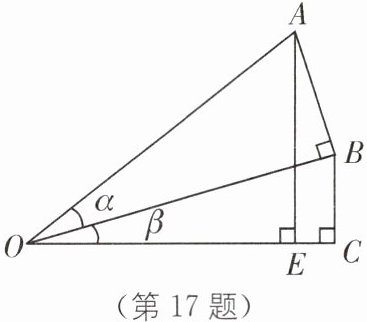
（2）若$\alpha$，$\beta$，$\alpha+\beta$都是锐角，猜想$\sin\alpha+\sin\beta$与$\sin(\alpha+\beta)$的大小关系；
（3）请借助如图的图形证明上述猜想。

答案：
(1)$\sin25^{\circ}+\sin46^{\circ}\approx0.423 + 0.719 = 1.142$，$\sin71^{\circ}\approx0.946$，
∴$\sin25^{\circ}+\sin46^{\circ}＞\sin71^{\circ}$。
(2)$\sin\alpha+\sin\beta＞\sin(\alpha+\beta)$。
(3)由图，可知$\sin\alpha+\sin\beta=\frac{AB}{OA}+\frac{BC}{OB}$， $\sin(\alpha+\beta)=\frac{AE}{OA}$。
∵$OA＞OB$，
∴$\frac{BC}{OB}＞\frac{BC}{OA}$，
∴$\frac{AB}{OA}+\frac{BC}{OB}＞\frac{AB}{OA}+\frac{BC}{OA}=\frac{AB + BC}{OA}$。
∵$AB + BC＞AE$，
∴$\frac{AB + BC}{OA}＞\frac{AE}{OA}$，
∴$\sin\alpha+\sin\beta＞\sin(\alpha+\beta)$。