《2025年课时训练九年级数学下册人教版江苏人民出版社》

14. 如图，在四边形ABCD中，AC平分∠BAD，BC⊥AC，CD⊥AD，且AB = 18，AC = 12.
(1)求AD和CD的长度；
(2)若DE⊥AC于点E，CF⊥AB于点F，求$\frac{DE}{CF}$的值.

答案：
(1) 因为$AC$平分$\angle BAD$，所以$\angle BAC=\angle CAD$。 因为$BC\perp AC$，$CD\perp AD$，所以$\angle ACB=\angle ADC = 90^{\circ}$。 所以$\triangle ABC\sim\triangle ACD$。 所以$\frac{AB}{AC}=\frac{AC}{AD}$，所以$AD=\frac{AC^2}{AB}=\frac{144}{18}=8$。 所以$CD=\sqrt{AC^2 - AD^2}=4\sqrt{5}$。
(2) 由
(1)，得$\triangle ABC\sim\triangle ACD$，因为$DE\perp AC$，$CF\perp AB$，所以$\frac{DE}{CF}=\frac{AC}{AB}=\frac{12}{18}=\frac{2}{3}$。

15. （2023·武汉洪山区模拟）如图，点A，B，C，D在一条直线上，CE与BF交于点G，∠A = ∠1，CE//DF.
(1)求证：∠E = ∠F；
(2)若AB∶BC∶CD = 2∶2∶1，直接写出$\frac{S_{四边形GCDF}}{S_{四边形ABGE}}$的值.

答案：
(1) 因为$CE// DF$，所以$\angle BCG=\angle D$。 因为$\angle A=\angle1$，所以$180^{\circ}-\angle BCG-\angle A = 180^{\circ}-\angle D-\angle1$，所以$\angle E=\angle F$。
(2) 因为$AB:BC:CD = 2:2:1$，所以$AC:BD = 4:3$。 因为$\angle BCG=\angle D$，$\angle A=\angle1$，所以$\triangle AEC\sim\triangle BFD$，所以$\frac{\triangle ACE的面积}{\triangle BDF的面积}=(\frac{AC}{BD})^2=\frac{16}{9}$。 令$\triangle ACE$的面积$ = 16x$，则$\triangle BDF$的面积$ = 9x$。 因为$\angle1=\angle A$，所以$BG// AE$，所以$\triangle CBG\sim\triangle CAE$，所以$\frac{\triangle CBG的面积}{\triangle CAE的面积}=(\frac{BC}{AC})^2=\frac{1}{4}$，所以$\triangle CBG$的面积$=\frac{1}{4}\times16x = 4x$，所以四边形$ABGE$的面积$ = 16x - 4x = 12x$，四边形$CDFG$的面积$ = 9x - 4x = 5x$，所以$\frac{S_{四边形 GCDF}}{S_{四边形 ABGE}}=\frac{5x}{12x}=\frac{5}{12}$。

16. [开放探究性问题]如图(1)，在△ABC中，AB = 2，D是AB上一点（不与点A，B重合），DE//BC，交AC于点E，连接CD. 设△ABC的面积为S，△DEC的面积为S'.
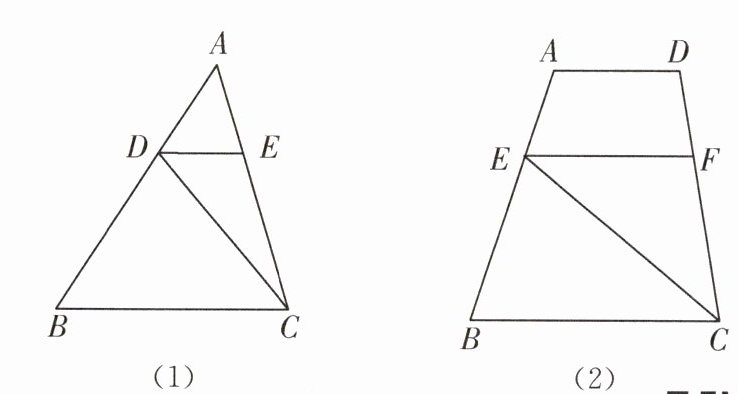
(1)当D是AB的中点时，求$\frac{S'}{S}$的值；
(2)若AD = x，$\frac{S'}{S}=y$，求y关于x的函数关系式以及自变量x的取值范围；
(3)如图(2)，在四边形ABCD中，AB = 2，AD//BC，$AD=\frac{1}{2}BC$，E是AB上一点（不与A，B重合），EF//BC，交CD于点F，连接CE. 设AE = a，四边形ABCD的面积为S，△EFC的面积为S'，请利用(2)的解法或结论，用含字母a的代数式表示$\frac{S'}{S}$.

答案：

(1) 因为$D$为$AB$的中点，所以$AB = 2AD$。 因为$DE// BC$，所以$\triangle ADE\sim\triangle ABC$，所以$\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{2}$，所以$AE = EC$。 因为$\triangle ADE$的边$AE$上的高和$\triangle DEC$的边$CE$上的高相等，所以$S_{\triangle ADE}=S_{\triangle DEC}=S'$。 因为$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{AD}{AB})^2=(\frac{1}{2})^2=\frac{1}{4}$，所以$\frac{S'}{S}=\frac{1}{4}$。
(2) 因为$DE// BC$，所以$\triangle ADE\sim\triangle ABC$，所以$\frac{AD}{AB}=\frac{AE}{AC}$，所以$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{AD}{AB})^2=(\frac{x}{2})^2=\frac{1}{4}x^2$ ①。 因为$AB = 2$，$AD = x$，所以$\frac{AE}{AC}=\frac{AD}{AB}=\frac{x}{2}$，所以$\frac{EC}{AE}=\frac{2 - x}{x}$。 因为$\triangle ADE$的边$AE$上的高和$\triangle DEC$的边$CE$上的高相等，所以$\frac{S_{\triangle DEC}}{S_{\triangle ADE}}=\frac{EC}{AE}=\frac{2 - x}{x}$ ②。 ①×②，得$\frac{S_{\triangle DEC}}{S_{\triangle ABC}}=\frac{1}{4}x^2\cdot\frac{2 - x}{x}$，所以$y=\frac{S'}{S}=\frac{S_{\triangle DEC}}{S_{\triangle ABC}}=-\frac{1}{4}x^2+\frac{1}{2}x$。 因为$AB = 2$，所以$x$的取值范围是$0\lt x\lt2$。 所以$y = -\frac{1}{4}x^2+\frac{1}{2}x(0\lt x\lt2)$。
(3) 如图，连接$AC$交$EF$于点$M$。因为$AB = 2$，$AE = a$，所以$BE = 2 - a$。 因为$AD// BC$且$AD=\frac{1}{2}BC$，所以$\frac{S_{\triangle ADC}}{S_{\triangle ABC}}=\frac{1}{2}$，所以$S_{\triangle ADC}=\frac{1}{2}S_{\triangle ABC}$。 因为四边形$ABCD$的面积为$S$，所以$S_{\triangle ADC}=\frac{1}{3}S$，$S_{\triangle ABC}=\frac{2}{3}S$。 由
(2)的结论可知，$\frac{S_{\triangle EMC}}{S_{\triangle ABC}}=-\frac{1}{4}a^2+\frac{1}{2}a$，所以$S_{\triangle EMC}=(\frac{-a^2 + 2a}{6})S$。 因为$AD// BC$，$EF// BC$，所以$AD// EF// BC$，所以$\triangle MFC\sim\triangle ADC$，$\frac{CF}{CD}=\frac{BE}{AB}=\frac{2 - a}{2}$，所以$\frac{S_{\triangle MFC}}{S_{\triangle ADC}}=(\frac{CF}{CD})^2=(\frac{2 - a}{2})^2$。 因为$S_{\triangle ADC}=\frac{1}{3}S$，所以$S_{\triangle MFC}=(\frac{a^2 - 4a + 4}{12})S$，所以$S_{\triangle EFC}=S_{\triangle EMC}+S_{\triangle MFC}=(\frac{-a^2 + 2a}{6})S+(\frac{a^2 - 4a + 4}{12})S=(-\frac{a^2}{12}+\frac{1}{3})S$。 因为$\triangle EFC$的面积为$S'$，所以$\frac{S'}{S}=-\frac{a^2}{12}+\frac{1}{3}$。