《2025年课时训练九年级数学下册人教版江苏人民出版社》

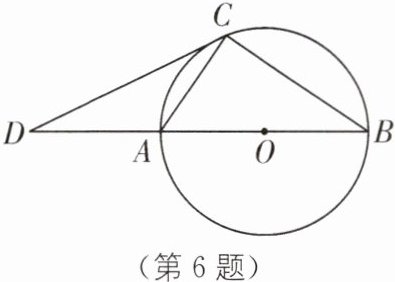
6 (2023·台州仙居二模)如图，$AB$是$\odot O$的直径，点$C$在$\odot O$上，点$D$在$BA$的延长线上，连接$CD$，$CA$，$CB$，且$DC^{2}=DA\cdot DB$.
(1)求证：$\triangle ACD\sim\triangle CBD$；
(2)判断直线$CD$与$\odot O$的位置关系，并说明理由.

答案：

(1)因为DC² = DA·DB，所以$\frac{CD}{AD}=\frac{BD}{CD}$. 因为∠D = ∠D，所以△ACD∽△CBD.
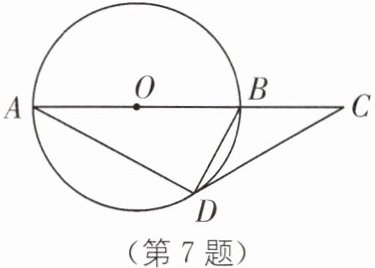
(2)直线CD与⊙O相切. 理由如下： 如图，连接OC. 因为△ACD∽△CBD，所以∠DCA = ∠B. 因为OB = OC，所以∠OCB = ∠B，所以∠DCA = ∠OCB. 因为AB是⊙O的直径，所以∠ACB = 90°， 所以∠DCO = ∠DCA + ∠ACO = ∠OCB + ∠ACO = 90°，所以OC⊥CD. 因为OC是半径，所以直线CD是⊙O的切线.

7 如图，$AB$是$\odot O$的直径，$CD$是$\odot O$的切线，$C$在$AB$的延长线上.
(1)求证：$\triangle CAD\sim\triangle CDB$；
(2)若$\angle C = 30^{\circ}$，$AC = 9$，求$\triangle DBC$的面积.

答案：

(1)如图，连接OD.因为OB = OD. 所以∠ODB = ∠ABD. 因为CD是⊙O的切线， 所以∠ODC = 90°，所以∠ODB + ∠CDB = 90°. 因为AB是⊙O的直径，所以∠ADB = 90°， 所以∠ABD + ∠BAD = 90°，所以∠CAD = ∠CDB. 因为∠C = ∠C，所以△CAD∽△CDB.
(2)因为∠ODC = 90°，∠C = 30°，所以OC = 2OD. 因为AB是⊙O的直径，AC = 9， 所以$OA = OB = OD=\frac{1}{2}OC = BC=\frac{1}{3}AC = 3$. 由
(1)，得△CAD∽△CDB， 所以$\frac{CD}{CB}=\frac{CA}{CD}$，所以CD² = CB·CA = 3×9 = 27， 所以$CD=\sqrt{27}=3\sqrt{3}$， 所以△OCD的面积=$\frac{1}{2}OD·CD=\frac{1}{2}×3×3\sqrt{3}=\frac{9\sqrt{3}}{2}$. 因为BC = OB， 所以△DBC的面积=$\frac{1}{2}$△OCD的面积=$\frac{9\sqrt{3}}{4}$.

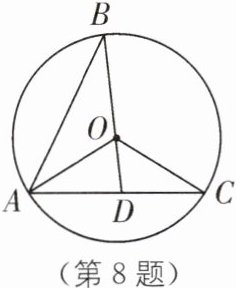
8 如图，已知$\odot O$的半径为$1$，$AB$，$AC$是$\odot O$的两条弦，且$AB = AC$，延长$BO$交$AC$于点$D$，连接$OA$，$OC$，若$AD^{2}=AB\cdot DC$，求$OD$的长.

答案： 在△AOB和△AOC中， 因为AB = AC，OB = OC，OA = OA， 所以△AOB≌△AOC(SSS)，所以∠ABO = ∠ACO. 因为OA = OC，所以∠ACO = ∠OAD. 所以∠ABO = ∠OAD. 因为∠ADO = ∠BDA，所以△ADO∽△BDA， 所以$\frac{AD}{BD}=\frac{OD}{AD}=\frac{AO}{AB}$. 设OD = x，则BD = 1 + x，所以$\frac{AD}{1 + x}=\frac{x}{AD}=\frac{1}{AB}$， 所以$AD=\sqrt{x(x + 1)}$，$AB=\frac{\sqrt{x(x + 1)}}{x}$. 因为DC = AC - AD = AB - AD，AD² = AB·DC， 所以$(\sqrt{x(x + 1)})²=\frac{\sqrt{x(x + 1)}}{x}(\frac{\sqrt{x(x + 1)}}{x}-\sqrt{x(x + 1)})$， 整理得(x² + x - 1)·(x + 1)=0， 解得$x=\frac{-1+\sqrt{5}}{2}$或$x=\frac{-1-\sqrt{5}}{2}$(舍去)或x = - 1(舍去)， 则$OD=\frac{\sqrt{5}-1}{2}$.

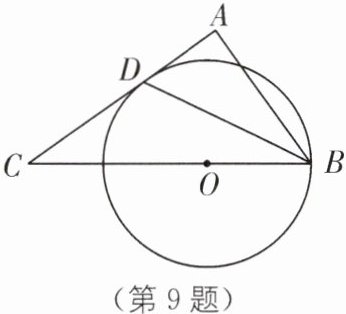
9 (2023·西安长安区一模)如图，在$Rt\triangle ABC$中，$\angle BAC = 90^{\circ}$，$O$为边$BC$上一点，以$OB$为半径的$\odot O$与$AC$相切于点$D$，连接$BD$.
(1)求证：$BD$平分$\angle ABC$；
(2)连接$AO$，若$\angle AOB = 90^{\circ}$，$AB = 4$，求$\odot O$的半径.

答案：

(1)如图，连接OD，则OD = OB，所以∠ODB = ∠CBD.!因为⊙O与AC相切于点D，所以AC⊥OD， 所以∠ODC = ∠BAC = 90°，所以DO//AB， 所以∠ODB = ∠ABD，所以∠CBD = ∠ABD， 所以BD平分∠ABC.
(2)设OB = DO = r. 因为OD//AB，所以△DOC∽△ABC， 所以$\frac{DO}{AB}=\frac{CO}{CB}$，∠COD = ∠ABO， 所以DO·CB = AB·CO. 因为DO = OB，∠ODC = ∠AOB = 90°， 所以△COD≌△ABO(ASA)，所以CO = AB = 4， 所以r(4 + r)=4×4， 解得$r_1 = 2\sqrt{5}-2$，$r_2=-2\sqrt{5}-2$(不符合题意，舍去)，所以⊙O的半径为$2\sqrt{5}-2$.