第30页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
6 如图,双曲线$y_1 = \frac{k_1}{x}$($k_1>0$)与直线$y_2 = k_2x + b$($k_2>0$)的一个交点的横坐标为$2$. 当$x = 3$时,$y_1$_______$y_2$.(填“$>$”“$<$”或“$=$”)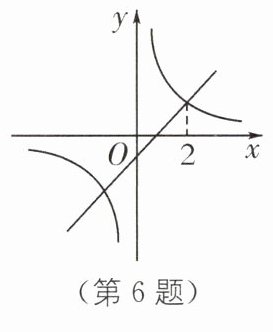

答案:
<
7(2023·沈阳模拟)如图,在平面直角坐标系中,$O$是坐标原点,反比例函数$y = \frac{k}{x}$($k \neq 0$)的图象交直线$y = - \frac{5}{12}x$于点$A$(点$A$在第四象限),若$OA = 13$,则$k$的值为_______.
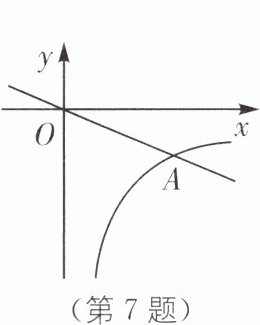

答案:
-60
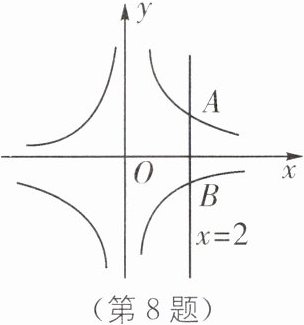
8 如图,直线$x = 2$与反比例函数$y = \frac{2}{x}$,$y = - \frac{1}{x}$的图象分别交于$A$,$B$两点,若点$P$是$y$轴上的任意一点,则$\triangle PAB$的面积是________.

答案:
$\frac{3}{2}$
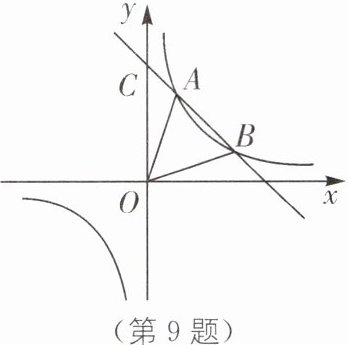
9(2023·菏泽巨野三模)如图,反比例函数$y = \frac{m}{x}$($m \neq 0$)与一次函数$y = kx + b$($k \neq 0$)的图象交于点$A(1,3)$,点$B(n,1)$,一次函数$y = kx + b$($k \neq 0$)与$y$轴相交于点$C$.
(1)求反比例函数和一次函数的解析式;
(2)连接$OA$,$OB$,求$\triangle OAB$的面积.
(1)求反比例函数和一次函数的解析式;
(2)连接$OA$,$OB$,求$\triangle OAB$的面积.

答案:
9. - (1)将$A(1,3)$代入$y = \frac{m}{x}$,得$m = 3$,所以反比例函数的解析式为$y = \frac{3}{x}$。将$B(n,1)$代入$y = \frac{3}{x}$,得$n = 3$,所以点$B$的坐标为$(3,1)$。将$A(1,3)$,$B(3,1)$代入$y = kx + b$,得$\begin{cases}k + b = 3\\3k + b = 1\end{cases}$,解得$\begin{cases}k = -1\\b = 4\end{cases}$,所以一次函数的解析式为$y = -x + 4$。 - (2)设一次函数$y = -x + 4$的图象与$x$轴交于点$D$。如图,过点$A$作$AE⊥y$轴于点$E$,过点$B$作$BF⊥x$轴于点$F$。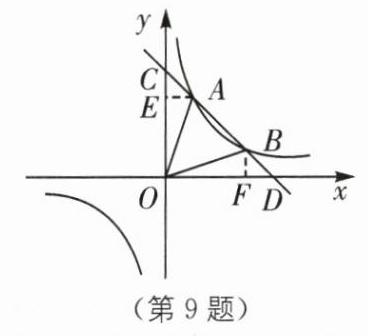
对于$y = -x + 4$,当$x = 0$时,$y = 4$,当$y = 0$时,$x = 4$,所以点$C(0,4)$,点$D(4,0)$,所以$OC = 4$,$OD = 4$。又点$A(1,3)$,$B(3,1)$,所以$AE = 1$,$BF = 1$,所以$S_{\triangle AOC}=\frac{1}{2}OC\cdot AE=\frac{1}{2}×4×1 = 2$,$S_{\triangle BOD}=\frac{1}{2}OD\cdot BF=\frac{1}{2}×4×1 = 2$。又$S_{\triangle OCD}=\frac{1}{2}OD\cdot OC=\frac{1}{2}×4×4 = 8$,所以$S_{\triangle OAB}=S_{\triangle OCD}-S_{\triangle AOC}-S_{\triangle BOD}=8 - 2 - 2 = 4$。
9. - (1)将$A(1,3)$代入$y = \frac{m}{x}$,得$m = 3$,所以反比例函数的解析式为$y = \frac{3}{x}$。将$B(n,1)$代入$y = \frac{3}{x}$,得$n = 3$,所以点$B$的坐标为$(3,1)$。将$A(1,3)$,$B(3,1)$代入$y = kx + b$,得$\begin{cases}k + b = 3\\3k + b = 1\end{cases}$,解得$\begin{cases}k = -1\\b = 4\end{cases}$,所以一次函数的解析式为$y = -x + 4$。 - (2)设一次函数$y = -x + 4$的图象与$x$轴交于点$D$。如图,过点$A$作$AE⊥y$轴于点$E$,过点$B$作$BF⊥x$轴于点$F$。

对于$y = -x + 4$,当$x = 0$时,$y = 4$,当$y = 0$时,$x = 4$,所以点$C(0,4)$,点$D(4,0)$,所以$OC = 4$,$OD = 4$。又点$A(1,3)$,$B(3,1)$,所以$AE = 1$,$BF = 1$,所以$S_{\triangle AOC}=\frac{1}{2}OC\cdot AE=\frac{1}{2}×4×1 = 2$,$S_{\triangle BOD}=\frac{1}{2}OD\cdot BF=\frac{1}{2}×4×1 = 2$。又$S_{\triangle OCD}=\frac{1}{2}OD\cdot OC=\frac{1}{2}×4×4 = 8$,所以$S_{\triangle OAB}=S_{\triangle OCD}-S_{\triangle AOC}-S_{\triangle BOD}=8 - 2 - 2 = 4$。
10 验光师测得一组关于近视眼镜的度数$y$(度)与镜片焦距$x$(米)的对应数据如表:
|镜片焦距$x$/米|1.00|0.50|0.25|0.20|0.10|
|----|----|----|----|----|----|
|近视眼镜的度数$y$/度|100|200|400|500|1000|
(1)请写出适当的函数解析式描述近视眼镜的度数$y$与镜片焦距$x$的关系;
(2)验光师测得小明同学的近视度数是250度,给小明配的眼镜的焦距应该是多少米?
|镜片焦距$x$/米|1.00|0.50|0.25|0.20|0.10|
|----|----|----|----|----|----|
|近视眼镜的度数$y$/度|100|200|400|500|1000|
(1)请写出适当的函数解析式描述近视眼镜的度数$y$与镜片焦距$x$的关系;
(2)验光师测得小明同学的近视度数是250度,给小明配的眼镜的焦距应该是多少米?
答案:
10. - (1)由表格中两个变量的对应值,得$100×1.00 = 200×0.50 = 400×0.25 = 500×0.20 = 1000×0.10 = 100$,所以$y$与$x$成反比例关系,所以$y$与$x$的函数解析式为$y = \frac{100}{x}$。 - (2)因为$y = 250$,所以$\frac{100}{x}=250$,所以$x = 0.4$。故给小明配的眼镜的焦距应该是$0.4$米。
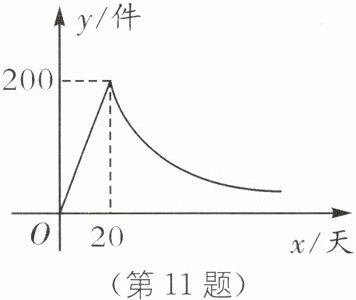
11(2023·辽宁大连金普新区期末)某种商品上市之初进行了大量的广告宣传,其日销售量$y$与上市的天数$x$之间成正比例函数关系,当广告停止后,日销售量$y$与上市的天数$x$之间成反比例函数关系(如图所示),现已知上市20天时,当日销售量为200件.
(1)求该商品上市以后日销售量$y$(件)与上市的天数$x$(天)之间的函数解析式;
(2)当上市的天数为多少时,日销售量为80件?
(1)求该商品上市以后日销售量$y$(件)与上市的天数$x$(天)之间的函数解析式;
(2)当上市的天数为多少时,日销售量为80件?

答案:
11. - (1)当$0 < x\leq20$时,设$y = k_1x$,把$(20,200)$代入得$k_1 = 10$,所以$y = 10x$;当$x > 20$时,设$y = \frac{k_2}{x}$,把$(20,200)$代入得$k_2 = 4000$,所以$y = \frac{4000}{x}$。故$y =\begin{cases}10x(0\leq x\leq20)\\\frac{4000}{x}(x > 20)\end{cases}$。 - (2)当$0 < x\leq20$时,令$y = 80$,即$80 = 10x$,解得$x = 8$;当$x > 20$时,令$y = 80$,即$80 = \frac{4000}{x}$,解得$x = 50$。故当上市的天数为$8$天或$50$天时,日销售量为$80$件。
查看更多完整答案,请扫码查看


