《2025年课时训练九年级数学下册人教版江苏人民出版社》

1. 如图，$a// b// c$，两条直线与这三条平行线分别交于点$A$，$B$，$C$和$D$，$E$，$F$. 已知$AB = 3$，$BC = 2$，$DE = 6$，则$DF$等于( ).

A. 4
B. 9
C. 10
D. 15

答案： **C** [解析] 因为 $a // b // c$，所以 $\frac{AB}{BC}=\frac{DE}{EF}$，即 $\frac{3}{2}=\frac{6}{EF}$。所以 $EF = 4$。所以 $DF = EF + DE = 4 + 6 = 10$。故选 C。

2. （2022·内江隆昌蓝天育才学校模拟）如图，$AD// EF// BC$，点$G$是$EF$的中点，$\frac{EF}{BC}=\frac{3}{5}$，若$EF = 6$，则$AD$的长为( ).

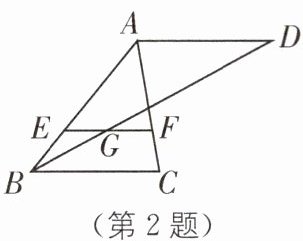
A. 6
B. $\frac{13}{2}$
C. 7
D. $\frac{15}{2}$

答案： **D** [解析] 因为 $EF // BC$，所以 $\frac{EF}{BC}=\frac{AE}{AB}=\frac{3}{5}$。所以 $\frac{BE}{AB}=\frac{2}{5}$。因为 $AD // EF$，所以 $\frac{EG}{AD}=\frac{BE}{AB}=\frac{2}{5}$。因为点 $G$ 是 $EF$ 的中点，$EF = 6$，所以 $EG = 3$。所以 $\frac{3}{AD}=\frac{2}{5}$。所以 $AD=\frac{15}{2}$。故选 D。

3. （2023·梅州蕉岭一模）如图，在$\triangle ABC$中，$D$，$E$为边$AB$的三等分点，$EF// DG// AC$，$H$为$AF$与$DG$的交点. 若$AC = 12$，则$DH =$_______.

答案： **2** [解析] 因为 $D$，$E$ 为边 $AB$ 的三等分点，$EF // DG // AC$，所以 $BE = DE = AD$，$BF = GF = CG$，$AH = HF$，所以 $AB = 3BE$，$DH$ 是 $\triangle AEF$ 的中位线，所以 $DH=\frac{1}{2}EF$。因为 $EF // AC$，所以 $\triangle BEF \sim \triangle BAC$，所以 $\frac{EF}{AC}=\frac{BE}{BA}$，即 $\frac{EF}{12}=\frac{BE}{3BE}$，解得 $EF = 4$，所以 $DH=\frac{1}{2}EF=\frac{1}{2}×4 = 2$。

4. （2022·安徽芜湖无为期中）如图，已知在$\triangle ABC$中，$AD$为$BC$上的中线，点$E$在$AD$上，且$\frac{DE}{AE}=\frac{1}{3}$，射线$CE$交$AB$于点$F$，求$\frac{AF}{FB}$的值.

答案：
如图，过点 $D$ 作 $DH // FC$ 交 $AB$ 于点 $H$， 则 $\frac{FH}{AF}=\frac{DE}{AE}=\frac{1}{3}$，$\frac{FH}{HB}=\frac{CD}{BD}=1$，所以 $\frac{AF}{FB}=\frac{3}{2}$。 解题关键：本题考查的是平行线分线段成比例定理，正确作出辅助线、灵活运用定理是解题的关键。

5. 下列可以判定$\triangle ABC\backsim\triangle A'B'C'$的条件是( ).
A. $\angle A=\angle B'=\angle C'$
B. $\frac{AB}{A'B'}=\frac{AC}{A'C'}$且$\angle A=\angle C'$
C. $\frac{AB}{A'B'}=\frac{AC}{A'C'}$且$\angle A=\angle A'$
D. 以上条件都不对

答案： **C** [解析] A. 只有一组角对应相等的两个三角形不一定相似，故 A 不符合题意；B. 两边对应成比例，但夹角不相等的两个三角形不一定相似，故 B 不符合题意；C. 两边对应成比例且夹角相等的两个三角形相似，故 C 符合题意。故选 C。

6. 如图，点$P$是$\triangle ABC$的边$AC$上一点，连接$BP$，添加下列条件，不能判定$\triangle ABC\backsim\triangle APB$的是( ).

A. $\angle C=\angle ABP$
B. $\angle ABC=\angle APB$
C. $\frac{AB}{AC}=\frac{AP}{AB}$
D. $\frac{AC}{BC}=\frac{AB}{PB}$

答案： **D** [解析] A. 因为 $\angle A=\angle A$，$\angle C=\angle ABP$，所以 $\triangle ABC \sim \triangle APB$，故本选项不合题意；B. 因为 $\angle A=\angle A$，$\angle ABC=\angle APB$，所以 $\triangle ABC \sim \triangle APB$，故本选项不合题意；C. 因为 $\angle A=\angle A$，$\frac{AB}{AC}=\frac{AP}{AB}$，所以 $\triangle ABP \sim \triangle ACB$，故本选项不合题意；D. 根据 $\frac{AC}{BC}=\frac{AB}{PB}$ 和 $\angle A=\angle A$ 不能判断 $\triangle ABP \sim \triangle ACB$，故本选项符合题意。故选 D。

7. （2023·哈尔滨一模）如图，在$\triangle ABC$中，$AD$是$\triangle ABC$的中线，$CE\perp AD$，垂足为$E$，$CE = 3$，$AB = 3\sqrt{10}$，$\angle BAD=\angle BCE$，则线段$AC$长为_______.

答案：
**$\sqrt{58}$** [解析] 如图，过点 $B$ 作 $BF \perp AD$，交 $AD$ 的延长线于点 $F$。 因为 $AD$ 是 $\triangle ABC$ 的中线，所以 $CD = BD$。因为 $CE \perp AD$，$BF \perp AD$，所以 $\angle CED=\angle BFD = 90^{\circ}$。在 $\triangle BDF$ 和 $\triangle CDE$ 中，$\begin{cases}\angle BFD=\angle CED\\\angle BDF=\angle CDE\\BD = CD\end{cases}$，所以 $\triangle BDF \cong \triangle CDE(AAS)$，所以 $BF = CE = 3$，$DF = DE$，$\angle DBF=\angle DCE$。在 $Rt\triangle ABF$ 中，$AF=\sqrt{AB^{2}-BF^{2}}=\sqrt{(3\sqrt{10})^{2}-3^{2}} = 9$。因为 $\angle BAD=\angle BCE$，所以 $\angle BAE=\angle DBF$。因为 $\angle DFB=\angle BFA$，所以 $\triangle FBD \sim \triangle FAB$，所以 $FD:FB = FB:FA$，即 $FD:3 = 3:9$，解得 $FD = 1$，所以 $DE = 1$，所以 $AE = AF - DE - DF = 7$。在 $Rt\triangle ACE$ 中，$AC=\sqrt{AE^{2}+CE^{2}}=\sqrt{7^{2}+3^{2}}=\sqrt{58}$。

8. （2023·上海宝安区二模）如图，在$Rt\triangle ABC$中，$\angle B = 90^{\circ}$，点$D$为$BC$中点，$\angle C = 2\angle BAD$，则$\frac{AD}{AC}$的值为_______.

答案：
**$\frac{\sqrt{6}}{3}$** [解析] 如图，延长 $CB$ 至点 $E$，使 $BE = BD$，连接 $AE$，设 $BD = a$，则 $DC = a$，$DE = 2a$。 由题意，得 $\angle ABD=\angle ABE$。因为 $AB = AB$，所以 $Rt\triangle ABD \cong Rt\triangle ABE(SAS)$，所以 $\angle E=\angle ADE$，$\angle BAD=\angle BAE$，$AE = AD$。因为 $\angle C = 2\angle BAD$，所以 $\angle C=\angle EAD$。因为 $\angle ADE=\angle C+\angle DAC$，$\angle EAC=\angle EAD+\angle DAC$，所以 $\angle E=\angle ADE=\angle EAC$，所以 $AC = CE = 3a$。因为 $\angle E=\angle ADE=\angle EAC$，$\angle C=\angle EAD$，所以 $\triangle ECA \sim \triangle EAD$，所以 $\frac{CA}{AD}=\frac{AE}{DE}=\frac{AD}{DE}$，即 $\frac{3a}{AD}=\frac{AD}{2a}$，所以 $AD=\sqrt{6}a$。又 $AC = 3a$，所以 $\frac{AD}{AC}=\frac{\sqrt{6}a}{3a}=\frac{\sqrt{6}}{3}$。

9. （2022·山东泰安岱岳区期末）如图，在$\triangle ABC$中，$\angle C = 90^{\circ}$，$AC = BC = 2$，点$O$为$AB$的中点，点$E$，$F$分别为$BC$，$AC$边上的动点.
(1)若点$E$，$F$分别为$BC$，$AC$的中点，求线段$EF$的长；
(2)若$\angle EOF = 45^{\circ}$，
①求证：$\triangle BOE\backsim\triangle AFO$；
②试问$\triangle BOE$与$\triangle EOF$相似吗？并说明理由.

答案：
(1) 因为 $E$，$F$ 分别为 $BC$，$AC$ 的中点，所以 $EF=\frac{1}{2}AB$。因为 $\angle C = 90^{\circ}$，$AC = BC = 2$，所以 $AB = 2\sqrt{2}$，所以 $EF=\sqrt{2}$。
(2) ① 因为 $\angle C = 90^{\circ}$，$AC = BC$，所以 $\angle A=\angle B = 45^{\circ}$。因为 $\angle EOF = 45^{\circ}$，所以 $\angle BOE+\angle AOF = 135^{\circ}$。又 $\angle BEO+\angle BOE = 135^{\circ}$，所以 $\angle BEO=\angle AOF$，所以 $\triangle BOE \sim \triangle AFO$。 ② $\triangle BOE$ 与 $\triangle EOF$ 相似。理由如下：由①，得 $\frac{OE}{OF}=\frac{BE}{OA}$。因为 $O$ 为 $AB$ 的中点，所以 $OA = OB$，所以 $\frac{OE}{OF}=\frac{BE}{OB}$，所以 $\frac{OB}{OF}=\frac{BE}{OE}$。又 $\angle B=\angle EOF = 45^{\circ}$，所以 $\triangle BOE \sim \triangle OFE$。