《2025年课时训练九年级数学下册人教版江苏人民出版社》

12 (2023·河北承德兴隆期中)如图，在Rt△ABC中，∠C = 90°，M是直角边AC上一点，MN⊥AB于点N，AN = 3，AM = 4，求cos B的值.

答案： 答案：
∵∠C = 90°，MN⊥AB，
∴∠C = ∠ANM = 90°。 又∠A = ∠A，
∴△AMN∽△ABC，
∴$\frac{AC}{AB}$ = $\frac{AN}{AM}$ = $\frac{3}{4}$。 设AC = 3x，AB = 4x， 由勾股定理，得BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{7}$x， 在Rt△ABC中，cos B = $\frac{BC}{AB}$ = $\frac{\sqrt{7}x}{4x}$ = $\frac{\sqrt{7}}{4}$。

13 如图，已知四边形ABCD为矩形，AB = 4 cm，BC = 6 cm，M是BC的中点，DE⊥AM，求tan∠ADE的值.

答案： 答案：
∵四边形ABCD为矩形，
∴∠B = 90°，AD//BC，
∴∠AMB = ∠DAE。
∵DE⊥AM，
∴∠DEA = ∠B = 90°，
∴△ABM∽△DEA，
∴$\frac{BM}{AB}$ = $\frac{AE}{DE}$。 又AB = 4 cm，BM = $\frac{1}{2}$BC = 3 cm，
∴tan∠ADE = $\frac{AE}{DE}$ = $\frac{BM}{AB}$ = $\frac{3}{4}$。

14 如图，点E是矩形ABCD中边CD上一点，△BCE沿BE折叠为△BFE，点F落在AD上.
(1)求证：△ABF∽△DFE；
(2)若sin∠DFE = $\frac{1}{3}$，求tan∠EBC的值.

答案： 答案：
(1)
∵四边形ABCD是矩形，
∴∠A = ∠D = ∠C = 90°。
∵△BCE沿BE折叠为△BFE，
∴∠BFE = ∠C = 90°，
∴∠AFB + ∠DFE = 180° - ∠BFE = 90°。 又∠AFB + ∠ABF = 90°，
∴∠ABF = ∠DFE，
∴△ABF∽△DFE。
(2)在Rt△DEF中，sin∠DFE = $\frac{DE}{EF}$ = $\frac{1}{3}$，
∴设DE = a，则EF = 3a，
∴DF = $\sqrt{EF^{2}-DE^{2}}$ = 2$\sqrt{2}$a。
∵△BCE沿BE折叠为△BFE，
∴CE = EF = 3a，∠EBC = ∠EBF，
∴AB = CD = DE + CE = 4a。 由
(1)知△ABF∽△DFE，
∴$\frac{EF}{BF}$ = $\frac{DF}{AB}$ = $\frac{2\sqrt{2}a}{4a}$ = $\frac{\sqrt{2}}{2}$，
∴tan∠EBF = $\frac{FE}{BF}$ = $\frac{\sqrt{2}}{2}$， tan∠EBC = tan∠EBF = $\frac{\sqrt{2}}{2}$。

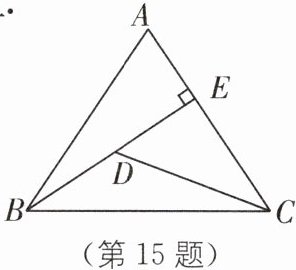
15 如图，在△ABC中，AB = AC = 10，tan A = 2，BE⊥AC于点E，D是线段BE上的一个动点，求CD + $\frac{\sqrt{5}}{5}$BD的最小值.

答案：
答案：如图，过点D作DH⊥AB于点H，过点C作CM⊥AB于点M。  
∵BE⊥AC，
∴∠AEB = 90°。 由tan A = $\frac{BE}{AE}$ = 2，可设AE = a，BE = 2a， 则有AB² = AE² + BE²，即100 = a² + 4a²，
∴a² = 20，解得a = 2$\sqrt{5}$或 - 2$\sqrt{5}$(舍)。
∴BE = 2a = 4$\sqrt{5}$。
∵AB = AC，BE⊥AC，CM⊥AB，
∴CM = BE = 4$\sqrt{5}$(等腰三角形两腰上的高相等)。
∵∠DBH = ∠ABE，∠BHD = ∠BEA，
∴sin∠DBH = $\frac{DH}{BD}$ = $\frac{AE}{AB}$ = $\frac{\sqrt{5}}{5}$，
∴DH = $\frac{\sqrt{5}}{5}$BD，
∴CD + $\frac{\sqrt{5}}{5}$BD = CD + DH。
∵CD + DH≥CM，
∴CD + $\frac{\sqrt{5}}{5}$BD≥4$\sqrt{5}$，
∴CD + $\frac{\sqrt{5}}{5}$BD的最小值为4$\sqrt{5}$。