《2025年课时训练九年级数学下册人教版江苏人民出版社》

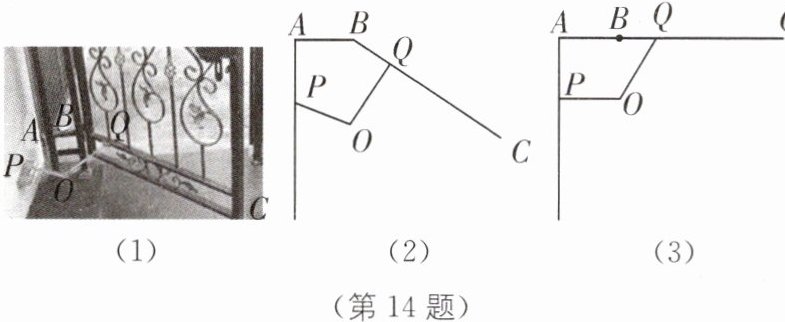
14. ［情境创新类问题］（2023·金华婺城区一模）图（1）是一款自动关门器，其示意图如图（2）所示. 固定铁架的宽$AB = 20\ cm$，支点$P$，$Q$分别固定在墙面和铁门上，$AP\perp AB$，$AP = 20\ cm$，摇臂$OP = 20\ cm$，连杆$OQ = 25\ cm$，点$A$，$B$，$O$，$P$，$Q$在同一平面内. 关门器工作时，点$C$绕点$B$转动，摇臂$OP$与连杆$OQ$长度均固定不变. 当铁门完全关闭时（如图（3）），点$A$，$B$，$Q$在同一直线上，$OP\perp AP$. 在开门的过程中，当端点$C$落在墙面$AP$上或连杆$OQ$落在$BC$上，都无法将门进一步打开，称此时为开门的极限状态.
(1)$BQ=$_______$cm$.
(2)为使在开门的极限状态下，连杆$OQ$落在$BC$上，则门宽$BC$的最大值为_______$cm$.

答案：

(1) **15** [解析] 如图
(1)，连接 $OB$。! 因为 $AP \perp AB$，$OP \perp AP$，所以 $AB // PO$，$\angle A=\angle APO = 90^{\circ}$。因为 $AB = AP = OP = 20 cm$，所以四边形 $ABOP$ 是正方形。所以 $\angle ABO = 90^{\circ}$，$OB = AP = 20 cm$，所以 $\angle OBQ = 90^{\circ}$。在 $Rt\triangle OBQ$ 中，$OQ = 25 cm$，所以 $BQ=\sqrt{OQ^{2}-OB^{2}}=\sqrt{25^{2}-20^{2}} = 15(cm)$。
(2) **$\frac{80\sqrt{7}+400}{9}$** [解析] 为使在开门的极限状态下，连杆 $OQ$ 落在 $BC$ 上，则门宽 $BC$ 取得最大值时，端点 $C$ 落在墙面 $AP$ 上，此时，$OB = OQ + BQ = 15 + 25 = 40(cm)$。如图
(2)，连接 $BP$，过点 $P$ 作 $PD \perp BC$ 于点 $D$，则 $\angle BDP=\angle CDP = 90^{\circ}$。 在 $Rt\triangle ABP$ 中，$BP=\sqrt{AB^{2}+AP^{2}}=\sqrt{20^{2}+20^{2}} = 20\sqrt{2}(cm)$，在 $Rt\triangle BDP$ 中，$PD^{2}=BP^{2}-BD^{2}=800 - BD^{2}$，在 $Rt\triangle ODP$ 中，$PD^{2}=OP^{2}-OD^{2}=400 - OD^{2}$，所以 $400 - OD^{2}=800 - BD^{2}$，即 $400 - OD^{2}=800-(40 - OD)^{2}$，所以 $OD = 15 cm$，所以 $PD=\sqrt{400 - OD^{2}} = 5\sqrt{7}(cm)$。因为 $\angle A=\angle CDP = 90^{\circ}$，$\angle ACB=\angle DCP$，所以 $\triangle ACB \sim \triangle DCP$，所以 $\frac{BC}{PC}=\frac{AC}{DC}=\frac{AB}{DP}=\frac{20}{5\sqrt{7}}$，所以 $PC=\frac{5\sqrt{7}}{20}BC=\frac{\sqrt{7}}{4}BC$，$DC=\frac{5\sqrt{7}}{20}AC=\frac{\sqrt{7}}{4}AC=\frac{\sqrt{7}}{4}(20 + PC)$，所以 $DC=\frac{\sqrt{7}}{4}(20+\frac{\sqrt{7}}{4}BC)=5\sqrt{7}+\frac{7}{16}BC$。在 $Rt\triangle CDP$ 中，$PD^{2}+CD^{2}=PC^{2}$，所以 $(5\sqrt{7})^{2}+(5\sqrt{7}+\frac{7}{16}BC)^{2}=(\frac{\sqrt{7}}{4}BC)^{2}$，所以 $BC=\frac{80\sqrt{7}\pm400}{9}$（负值不合题意，舍去），所以 $BC=\frac{80\sqrt{7}+400}{9}cm$，即门宽 $BC$ 的最大值为 $\frac{80\sqrt{7}+400}{9}cm$。

15. ［情境创新类问题］如图是一个小商场的纵截面图（矩形$ABCD$），$AD$是商场的顶部，$BC$是商场的地面，地面由边长为$80\ cm$的正方形瓷砖铺成，从$B$到$C$共有$25$块瓷砖，$AB$和$CD$是商场的两面墙壁，$MN$是顶部正中央的一个长方形的灯饰（$AM = DN$），小张同学想通过学过的几何知识来测量该商场的高度（$AB$）和灯饰的长度（$MN$），于是去商场时带了一块镜子和一根激光笔，他先把激光笔挂在墙壁$CD$距地面两块砖高度（$CG$的长）的$G$处，镜子水平放在地面距离$C$两块砖的$F$处，发现激光笔的反射光照到了$N$处；再把激光笔挂在墙壁$AB$距地面两块砖高度（$LB$的长）的$L$处，镜子水平放在地面距离$B$三块砖的$P$处，发现激光笔的反射光恰好又照到了$N$处，请你帮忙计算$AB$的高度和$MN$的长度.

答案：
如图，过点 $N$ 作 $NT \perp BC$ 于点 $T$，则四边形 $ABTN$，四边形 $CDNT$ 都是矩形，设 $AB = NT = CD = x cm$。由题意，得 $BC = 80×25 = 2000(cm)$，$CG = CF = LB = 2×80 = 160(cm)$，$BP = 3×80 = 240(cm)$。因为 $\angle B=\angle PTN = 90^{\circ}$，$\angle NPT=\angle LPB$，所以 $\triangle LBP \sim \triangle NTP$。所以 $\frac{LB}{NT}=\frac{PB}{PT}$。所以 $\frac{160}{x}=\frac{240}{PT}$。所以 $PT=\frac{3}{2}x$。同理，$\triangle GCF \sim \triangle NTF$，可得 $FT = NT = x$。因为 $BP + PT+TF + CF = 2000$，所以 $240+\frac{3}{2}x+x + 160 = 2000$。所以 $x = 640$。所以 $DN = CT = 640 + 160 = 800(cm)$，$AB = CD = 640 cm$。所以 $AM = DN = 800 cm$。所以 $MN = AD - AM - DN = 2000 - 1600 = 400(cm)$。故 $AB$ 的高度为 $640 cm$，$MN$ 的长度为 $400 cm$。

16. ［情境创新类问题］小丽和小明想测量河对岸一建筑物$AB$的高度. 如图，他们先在地面上放一平面平面镜$E$，小丽在射线$AE$上调整自己与镜子的距离，直到刚好能从镜子中看到建筑物的顶端$B$，此时她与镜子的距离$CE = 2$米，然后小明在距离建筑物$6$米处安装了一个测倾器$GH$，测得$\angle HGE = 60^{\circ}$，若小丽的眼睛距离地面高度$CD = 1.6$米，$GH = 1$米，$AB\perp AC$，$GH\perp AC$，$DC\perp AC$，点$A$，$H$，$E$，$C$在同一条直线上. 请你利用这些数据，求建筑物的高度$AB$.（结果精确到$0.1$米，参考数据：$\sqrt{2}\approx1.414$，$\sqrt{3}\approx1.732$）

答案： 由题意，得 $AH = 6$ 米。因为 $AB \perp AC$，$GH \perp AC$，$DC \perp AC$，所以 $\angle BAE=\angle DCE=\angle GHE = 90^{\circ}$。在 $Rt\triangle GHE$ 中，$\angle HGE = 60^{\circ}$，$GH = 1$ 米，所以 $GE = 2HG = 2$ 米，所以 $EH=\sqrt{GE^{2}-GH^{2}}=\sqrt{3}$（米），所以 $AE = AH + EH=(6+\sqrt{3})$ 米。因为 $\angle AEB=\angle CED$，$\angle BAE=\angle DCE = 90^{\circ}$，所以 $\triangle ABE \sim \triangle CDE$，所以 $\frac{AB}{CD}=\frac{AE}{CE}$，即 $\frac{AB}{1.6}=\frac{6+\sqrt{3}}{2}$，解得 $AB = 4.8 + 0.8\sqrt{3}\approx6.2$（米）。故建筑物的高度 $AB$ 约为 $6.2$ 米。