《2025年课时训练九年级数学下册人教版江苏人民出版社》

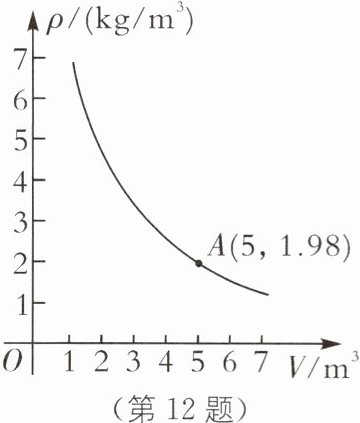
12 [跨学科综合](2023·江苏连云港海州区期末)密闭容器内有一定质量的二氧化碳，当容器的体积$V$(单位：$m^{3}$)变化时，气体的密度$\rho$(单位：$kg/m^{3}$)也随之变化. 已知密度$\rho$与体积$V$是反比例函数关系，它的图象如图所示.
(1)求密度$\rho$与体积$V$的函数解析式；
(2)当$\rho = 3$时，求$V$的值；
(3)当密闭容器的体积不能超过$9\ m^{3}$，直接写出密度$\rho$的取值范围.

答案： （1）设密度ρ关于体积V的函数解析式为$ρ = \frac{k}{V}$(k≠0)。
∵当V = 5 m³时，ρ = 1.98 kg/m³，
∴1.98 = $\frac{k}{5}$，
∴k = 9.9， 故密度ρ与体积V的函数解析式为$ρ = \frac{9.9}{V}$(V＞0)。 （2）把ρ = 3代入$ρ = \frac{9.9}{V}$，得3 = $\frac{9.9}{V}$，
∴V = 3.3 m³。 （3）
∵$ρ = \frac{9.9}{V}$(V＞0)，
∴$V = \frac{9.9}{\rho}$(ρ＞0)。
∵V≤9，
∴$\frac{9.9}{\rho}≤9$，
∴ρ≥1.1。 故密度ρ的取值范围为ρ≥1.1。

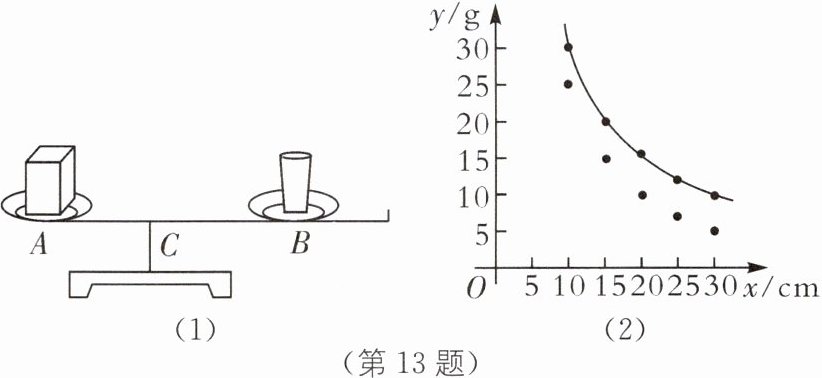
13 (2023·郴州中考)在实验课上，小明做了一个试验. 如图(1)，在仪器左边托盘$A$(固定)中放置一个物体，在右边托盘$B$(可左右移动)中放置一个可以装水的容器，容器的质量为$5\ g$. 在容器中加入一定质量的水，可以使仪器左右平衡. 改变托盘$B$与点$C$的距离$x(cm)(0 ＜ x\leqslant60)$，记录容器中加入的水的质量，得到下表：
| 托盘$B$与点$C$的距离$x/cm$ | 30 | 25 | 20 | 15 | 10 |
| ---- | ---- | ---- | ---- | ---- | ---- |
| 容器与水的总质量$y_{1}/g$ | 10 | 12 | 15 | 20 | 30 |
| 加入的水的质量$y_{2}/g$ | 5 | 7 | 10 | 15 | 25 |
把上表中的$x$与$y_{1}$各组对应值作为点的坐标，在平面直角坐标系中描出这些点，并用光滑的曲线连接起来，得到如图(2)所示的$y_{1}$关于$x$的函数图象.
(1)请在该平面直角坐标系中作出$y_{2}$关于$x$的函数图象；
(2)观察函数图象，并结合表中的数据：
①猜测$y_{1}$与$x$之间的函数关系，并求$y_{1}$关于$x$的函数解析式；
②求$y_{2}$关于$x$的函数解析式；
③当$0 ＜ x\leqslant60$时，$y_{1}$随$x$的增大而______(填“增大”或“减小”)，$y_{2}$随$x$的增大而______(填“增大”或“减小”)，$y_{2}$的图象可以由$y_{1}$的图象向______(以“上”或“下”或“左”或“右”)平移得到.
(3)若在容器中加入的水的质量$y_{2}(g)$满足$19\leqslant y_{2}\leqslant45$，求托盘$B$与点$C$的距离$x(cm)$的取值范围.

答案：
（1）作出y₂关于x的函数图象如图：（2）①观察表格可知，y₁是x的反比例函数。 设$y_1 = \frac{k}{x}$，把(30, 10)代入得10 = $\frac{k}{30}$，
∴k = 300。 故y₁关于x的函数解析式是$y_1 = \frac{300}{x}$。 ②
∵y₁ = y₂ + 5，
∴$y_2 + 5 = \frac{300}{x}$，
∴$y_2 = \frac{300}{x} - 5$。 ③减小 减小 下 [解析]观察图象可得，当0＜x≤60时，y₁随x的增大而减小，y₂随x的增大而减小，y₂的图象可以由y₁的图象向下平移得到。 （3）
∵$y_2 = \frac{300}{x} - 5$，19≤y₂≤45，
∴19≤$\frac{300}{x} - 5$≤45，
∴24≤$\frac{300}{x}$≤50，
∴6≤x≤12.5。故托盘B与点C的距离x的取值范围为6≤x≤12.5。