第32页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
16(2023·泰安六中二模)如图,在平面直角坐标系$xOy$中,一次函数$y = 2x + 4$的图象与反比例函数$y = \frac{k}{x}$的图象相交于$A(a,-2)$,$B$两点.
(1)求反比例函数的解析式;
(2)求$\triangle AOB$的面积;
(3)在反比例函数第一象限图象上是否存在一点$C$,使得$\triangle ABC$的面积是$\triangle AOB$面积的一半? 如果存在,请直接写出点$C$的横坐标.
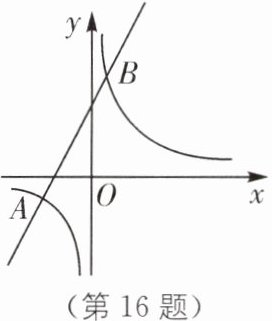
(1)求反比例函数的解析式;
(2)求$\triangle AOB$的面积;
(3)在反比例函数第一象限图象上是否存在一点$C$,使得$\triangle ABC$的面积是$\triangle AOB$面积的一半? 如果存在,请直接写出点$C$的横坐标.

答案:
16. - (1)因为一次函数图象经过点$A(a,-2)$,所以$2a + 4 = -2$,解得$a = -3$,所以$A(-3,-2)$。因为$y = \frac{k}{x}$的图象经过点$A(-3,-2)$,所以$k = -3×(-2)=6$,故反比例函数的解析式为$y = \frac{6}{x}$。 - (2)联立$\begin{cases}y = 2x + 4\\y = \frac{6}{x}\end{cases}$,解得$\begin{cases}x = -3\\y = -2\end{cases}$或$\begin{cases}x = 1\\y = 6\end{cases}$,所以$B(1,6)$。设直线$y = 2x + 4$与$x$轴相交于点$D$,连接$OA$,$OB$,如图(1)。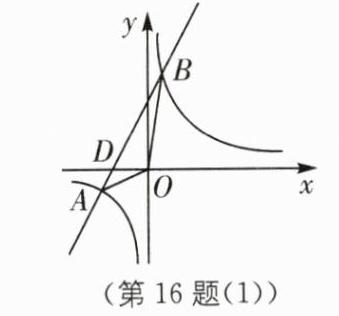
令$y = 0$,则$2x + 4 = 0$,解得$x = -2$,所以$D(-2,0)$,所以$OD = 2$。所以$S_{\triangle AOB}=S_{\triangle BOD}+S_{\triangle AOD}=\frac{1}{2}OD\cdot|y_B|+\frac{1}{2}OD\cdot|y_A|=\frac{1}{2}×2×6+\frac{1}{2}×2×2 = 8$。 - (3)存在,点$C$的横坐标为$\frac{-1+\sqrt{13}}{2}$或$\frac{-3+\sqrt{21}}{2}$。设直线$y = 2x + 4$与$y$轴相交于点$M$。令$x = 0$,则$y = 4$,所以$M(0,4)$。如图(2),过点$O$作$l_1∥AB$,在点$M$的下方取点$N$,使得$MN = \frac{1}{2}OM$,过点$N$作$l_2∥AB$与反比例函数在第一象限相交于点$C$,连接$AC$,$BC$,此时$l_2$到$AB$的距离是$l_1$到$AB$的距离的一半,即点$C$到$AB$的距离是点$O$到$AB$的距离的一半,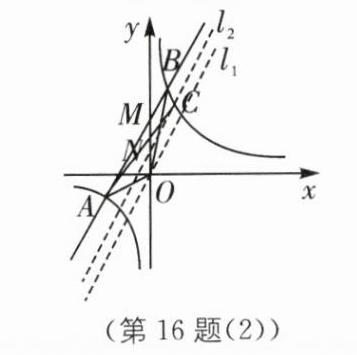
所以$S_{\triangle ABC}=\frac{1}{2}S_{\triangle AOB}$。因为$N$是$OM$的中点,所以$N(0,2)$。因为$l_2∥AB$,且经过点$N$,所以$l_2$的解析式为$y = 2x + 2$。联立$\begin{cases}y = 2x + 2\\y = \frac{6}{x}\end{cases}$,整理,得$x^2 + x - 3 = 0$,解得$x = \frac{-1-\sqrt{13}}{2}$或$x = \frac{-1+\sqrt{13}}{2}$。因为点$C$在第一象限,所以点$C$的横坐标为$\frac{-1+\sqrt{13}}{2}$;如图(3),在点$M$的上方取点$P$,使得$PM = \frac{1}{2}OM$,过点$O$作$l_1∥AB$,过点$P$作$l_3∥AB$与反比例函数在第一象限相交于点$C$,连接$AC$,$BC$,此时$l_3$到$AB$的距离是$l_1$到$AB$的距离的一半,即点$C$到$AB$的距离是点$O$到$AB$的距离的一半。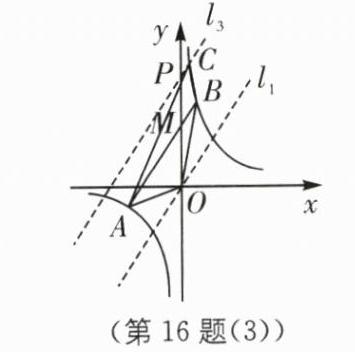
同理可得,$l_3$的解析式为$y = 2x + 6$。联立$\begin{cases}y = 2x + 6\\y = \frac{6}{x}\end{cases}$,整理,得$x^2 + 3x - 3 = 0$,解得$x = \frac{-3-\sqrt{21}}{2}$或$x = \frac{-3+\sqrt{21}}{2}$,因为点$C$在第一象限,所以点$C$的横坐标为$\frac{-3+\sqrt{21}}{2}$。综上可知,存在一点$C$,使得$\triangle ABC$的面积是$\triangle AOB$面积的一半,点$C$的横坐标为$\frac{-1+\sqrt{13}}{2}$或$\frac{-3+\sqrt{21}}{2}$。
16. - (1)因为一次函数图象经过点$A(a,-2)$,所以$2a + 4 = -2$,解得$a = -3$,所以$A(-3,-2)$。因为$y = \frac{k}{x}$的图象经过点$A(-3,-2)$,所以$k = -3×(-2)=6$,故反比例函数的解析式为$y = \frac{6}{x}$。 - (2)联立$\begin{cases}y = 2x + 4\\y = \frac{6}{x}\end{cases}$,解得$\begin{cases}x = -3\\y = -2\end{cases}$或$\begin{cases}x = 1\\y = 6\end{cases}$,所以$B(1,6)$。设直线$y = 2x + 4$与$x$轴相交于点$D$,连接$OA$,$OB$,如图(1)。

令$y = 0$,则$2x + 4 = 0$,解得$x = -2$,所以$D(-2,0)$,所以$OD = 2$。所以$S_{\triangle AOB}=S_{\triangle BOD}+S_{\triangle AOD}=\frac{1}{2}OD\cdot|y_B|+\frac{1}{2}OD\cdot|y_A|=\frac{1}{2}×2×6+\frac{1}{2}×2×2 = 8$。 - (3)存在,点$C$的横坐标为$\frac{-1+\sqrt{13}}{2}$或$\frac{-3+\sqrt{21}}{2}$。设直线$y = 2x + 4$与$y$轴相交于点$M$。令$x = 0$,则$y = 4$,所以$M(0,4)$。如图(2),过点$O$作$l_1∥AB$,在点$M$的下方取点$N$,使得$MN = \frac{1}{2}OM$,过点$N$作$l_2∥AB$与反比例函数在第一象限相交于点$C$,连接$AC$,$BC$,此时$l_2$到$AB$的距离是$l_1$到$AB$的距离的一半,即点$C$到$AB$的距离是点$O$到$AB$的距离的一半,

所以$S_{\triangle ABC}=\frac{1}{2}S_{\triangle AOB}$。因为$N$是$OM$的中点,所以$N(0,2)$。因为$l_2∥AB$,且经过点$N$,所以$l_2$的解析式为$y = 2x + 2$。联立$\begin{cases}y = 2x + 2\\y = \frac{6}{x}\end{cases}$,整理,得$x^2 + x - 3 = 0$,解得$x = \frac{-1-\sqrt{13}}{2}$或$x = \frac{-1+\sqrt{13}}{2}$。因为点$C$在第一象限,所以点$C$的横坐标为$\frac{-1+\sqrt{13}}{2}$;如图(3),在点$M$的上方取点$P$,使得$PM = \frac{1}{2}OM$,过点$O$作$l_1∥AB$,过点$P$作$l_3∥AB$与反比例函数在第一象限相交于点$C$,连接$AC$,$BC$,此时$l_3$到$AB$的距离是$l_1$到$AB$的距离的一半,即点$C$到$AB$的距离是点$O$到$AB$的距离的一半。

同理可得,$l_3$的解析式为$y = 2x + 6$。联立$\begin{cases}y = 2x + 6\\y = \frac{6}{x}\end{cases}$,整理,得$x^2 + 3x - 3 = 0$,解得$x = \frac{-3-\sqrt{21}}{2}$或$x = \frac{-3+\sqrt{21}}{2}$,因为点$C$在第一象限,所以点$C$的横坐标为$\frac{-3+\sqrt{21}}{2}$。综上可知,存在一点$C$,使得$\triangle ABC$的面积是$\triangle AOB$面积的一半,点$C$的横坐标为$\frac{-1+\sqrt{13}}{2}$或$\frac{-3+\sqrt{21}}{2}$。
17(2022·临沂中考)杠杆原理在生活中被广泛应用(杠杆原理:阻力$\times$阻力臂$=$动力$\times$动力臂),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图(1)).制作方法如下:
第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1 cm),确定支点$O$,并用细麻绳固定,在支点$O$左侧2 cm的$A$处固定一个金属吊钩,作为秤钩;
第二步:取一个质量为0.5 kg的金属物体作为秤砣.
(1)图(1)中,把重物挂在秤钩上,秤砣挂在支点$O$右侧的$B$处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,$OB$的长度随之变化.设重物的质量为$x$ kg,$OB$的长为$y$ cm.写出$y$关于$x$的函数解析式.若$0 < y < 48$,求$x$的取值范围;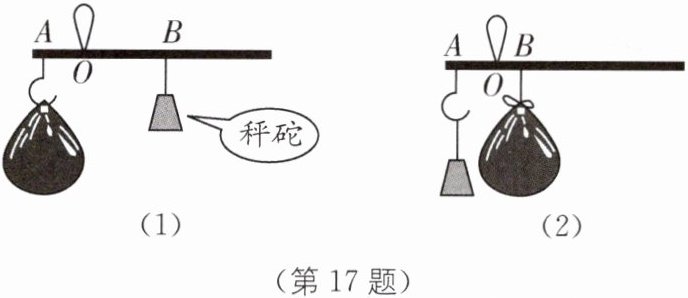
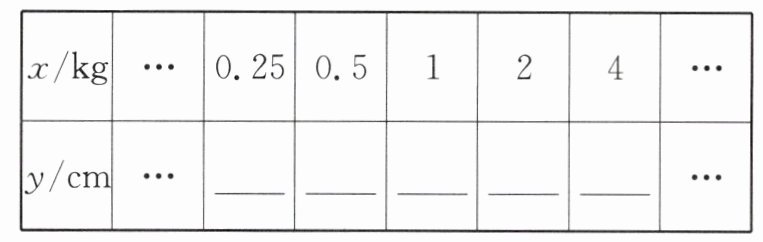
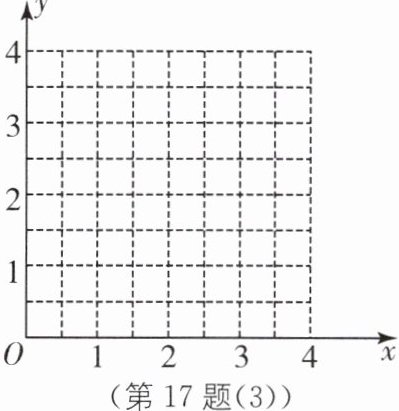
(2)调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点$O$右侧的$B$处,使秤杆平衡,如图(2).设重物的质量为$x$ kg,$OB$的长为$y$ cm,写出$y$关于$x$的函数解析式,完成下表,画出该函数的图象.
第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1 cm),确定支点$O$,并用细麻绳固定,在支点$O$左侧2 cm的$A$处固定一个金属吊钩,作为秤钩;
第二步:取一个质量为0.5 kg的金属物体作为秤砣.
(1)图(1)中,把重物挂在秤钩上,秤砣挂在支点$O$右侧的$B$处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,$OB$的长度随之变化.设重物的质量为$x$ kg,$OB$的长为$y$ cm.写出$y$关于$x$的函数解析式.若$0 < y < 48$,求$x$的取值范围;

(2)调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点$O$右侧的$B$处,使秤杆平衡,如图(2).设重物的质量为$x$ kg,$OB$的长为$y$ cm,写出$y$关于$x$的函数解析式,完成下表,画出该函数的图象.


答案:
17. - (1)因为阻力×阻力臂 = 动力×动力臂,所以重物×$OA$ = 秤砣的质量×$OB$。因为$OA = 2cm$,重物的质量为$xkg$,$OB$的长为$ycm$,秤砣的质量为$0.5kg$,所以$2x = 0.5y$,所以$y = 4x$。因为$4 > 0$,所以$y$随$x$的增大而增大。因为当$y = 0$时,$x = 0$;当$y = 48$时,$x = 12$,所以$0 < x < 12$。 - (2)因为阻力×阻力臂 = 动力×动力臂,所以秤砣的质量×$OA$ = 重物的质量×$OB$。因为$OA = 2cm$,重物的质量为$xkg$,$OB$的长为$ycm$,秤砣的质量为$0.5kg$,所以$2×0.5 = xy$,所以$y = \frac{1}{x}$。当$x = 0.25$时,$y = \frac{1}{0.25}=4$;当$x = 0.5$时,$y = \frac{1}{0.5}=2$;当$x = 1$时,$y = 1$;当$x = 2$时,$y = \frac{1}{2}$;当$x = 4$时,$y = \frac{1}{4}$。作函数图象如图。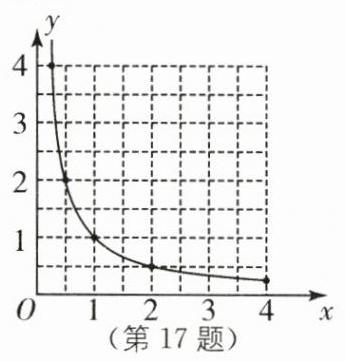
- 方法技巧:利用描点法(列表、描点、连线)画函数图象,利用实际问题中两个变量的关系确定函数模型,求出函数解析式。
17. - (1)因为阻力×阻力臂 = 动力×动力臂,所以重物×$OA$ = 秤砣的质量×$OB$。因为$OA = 2cm$,重物的质量为$xkg$,$OB$的长为$ycm$,秤砣的质量为$0.5kg$,所以$2x = 0.5y$,所以$y = 4x$。因为$4 > 0$,所以$y$随$x$的增大而增大。因为当$y = 0$时,$x = 0$;当$y = 48$时,$x = 12$,所以$0 < x < 12$。 - (2)因为阻力×阻力臂 = 动力×动力臂,所以秤砣的质量×$OA$ = 重物的质量×$OB$。因为$OA = 2cm$,重物的质量为$xkg$,$OB$的长为$ycm$,秤砣的质量为$0.5kg$,所以$2×0.5 = xy$,所以$y = \frac{1}{x}$。当$x = 0.25$时,$y = \frac{1}{0.25}=4$;当$x = 0.5$时,$y = \frac{1}{0.5}=2$;当$x = 1$时,$y = 1$;当$x = 2$时,$y = \frac{1}{2}$;当$x = 4$时,$y = \frac{1}{4}$。作函数图象如图。

- 方法技巧:利用描点法(列表、描点、连线)画函数图象,利用实际问题中两个变量的关系确定函数模型,求出函数解析式。
查看更多完整答案,请扫码查看


