《2025年课时训练九年级数学下册人教版江苏人民出版社》

1 小云沿着倾斜角为α的斜坡前进30 m，那么她上升的高度为( )．
A. $\frac{30}{\tan\alpha}$ m
B. 30tanα m
C. 30cosα m
D. 30sinα m

答案： D

2 (2023·温州平阳实验中学三模)如图是楼梯示意图，BC⊥AC，∠BAC =α，AC = 6米，则楼梯的高度BC是( )．

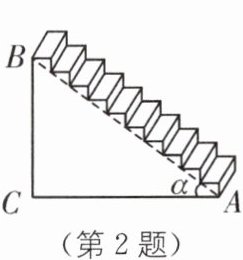
(第2题) (第3题)
A. 6tanα米
B. 6cosα米
C. 6sinα米
D. $\frac{6}{\sin\alpha}$米

答案： A

3 (2023·淄博临淄区一模)如图，衣架可以近似看成一个等腰三角形ABC，其中AB = AC，∠BAC = 126°，BC = 44 cm，则高AD约为( )．(sin27°≈0.45，cos27°≈0.89，tan27°≈0.51)

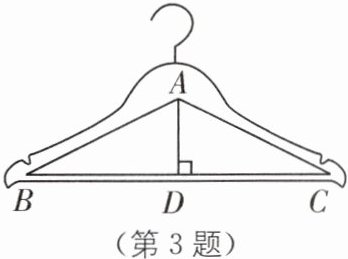
A. 9.90 cm
B. 11.22 cm
C. 19.58 cm
D. 22.44 cm

答案： B

4 (2023·长春南关区一模)如图，某停车场入口的栏杆AB，从水平位置绕点O旋转到A′B′的位置，已知AO的长为6米. 若栏杆的旋转角∠AOA′ =α，则栏杆A端升高的高度为( )．

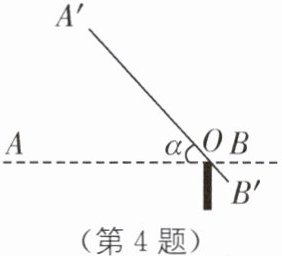
(第4题) (第5题)
A. 6sinα米
B. 6cosα米
C. $\frac{6}{\sin\alpha}$米
D. $\frac{6}{\cos\alpha}$米

答案： A

5 (2023·滕州三模)在水光潋滟的墨子湖畔，枣庄市首条湖底隧道建设格外受人关注. 如图，沿AB方向修建隧道箱体，为加快施工进度，在直线AB上湖的另一边的D处同时施工，取∠ABC = 150°，BC = 1 600 m，∠BCD = 105°，则C，D两点的距离是________m.

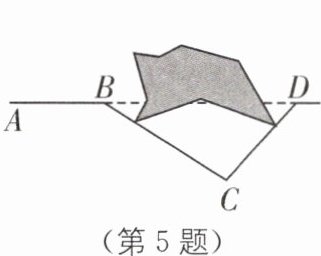
答案： $800\sqrt{2}$

6 若河岸的两边平行，河宽为900米，一只船由河岸的A处沿直线方向开往对岸的B处，AB与河岸的夹角是60°，船的速度为5米/秒，求船从A到B处约需多长时间. (参考数据：$\sqrt{3}$≈1.7)

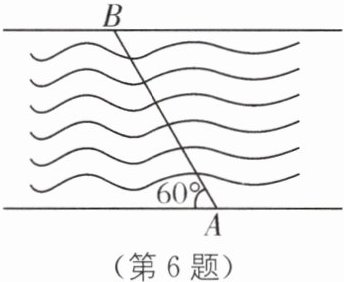
(第6题)

答案： 过点B作BC垂直河岸，垂足为C. 在Rt△ACB中，$AB = \frac{BC}{\sin\angle BAC}=\frac{900}{\sin60^{\circ}} = 600\sqrt{3}$（米）. 故时间$t=\frac{600\sqrt{3}}{5\times60}=2\sqrt{3}\approx3.4$（分）. 即船从A处到B处约需3.4分.

7 (2023·十堰张湾区模拟)如图，数学活动小组要测量学校楼房CD的高度，在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°，向前走20米到达A′处，测得点D的仰角为67.5°，已知测倾器AB的高度为1.6米，则楼房CD的高度约为( )．(结果精确到0.1米，参考数据：tan67.5° = 1 + $\sqrt{2}$，$\sqrt{2}$≈1.414)

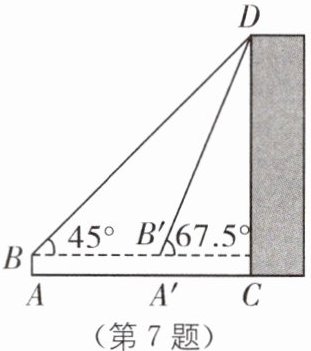
(第7题) 

A. 35.7米
B. 34.7米
C. 35.1米
D. 34.1米

答案： A