《2025年课时训练九年级数学下册人教版江苏人民出版社》

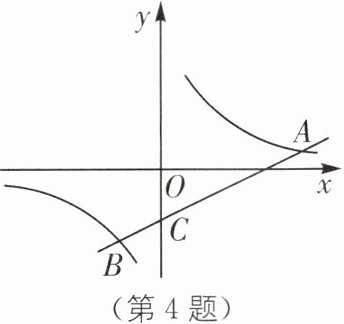
4 如图，在平面直角坐标系中，一次函数$y_1 = k_1x + b(k_1\neq0)$的图象与反比例函数$y_2=\frac{k_2}{x}(k_2\neq0)$的图象交于$A(8,1)$，$B(-2,a)$两点，与$y$轴交于点$C$.
(1)求一次函数的解析式；
(2)若点$D$在$y$轴上，且$S_{\triangle ABD}=20$，求点$D$的坐标.

答案：
 4.
(1) 因为点 \(A(8,1)\) 在反比例函数 \(y_2=\frac{k_2}{x}\) 上， 所以 \(1=\frac{k_2}{8}\)，所以 \(k_2 = 8\)，所以反比例函数的解析式为 \(y_2=\frac{8}{x}\)。 因为点 \(B(-2,a)\) 在反比例函数 \(y_2=\frac{8}{x}\) 的图象上， 所以 \(a=\frac{8}{-2}\)，所以 \(a=-4\)，所以 \(B(-2,-4)\)。 因为点 \(A\)，\(B\) 在一次函数 \(y_1 = k_1x + b\) 的图象上， 所以 \(\begin{cases}8k_1 + b = 1\\-2k_1 + b=-4\end{cases}\)，解得 \(\begin{cases}k_1=\frac{1}{2}\\b=-3\end{cases}\)， 所以一次函数的解析式为 \(y_1=\frac{1}{2}x - 3\)。
(2) 如图所示
，设点 \(D(0,d)\)。 因为点 \(C\) 是一次函数 \(y_1=\frac{1}{2}x - 3\) 与 \(y\) 轴的交点， 所以 \(C(0,-3)\)，所以 \(CD=\vert d + 3\vert\)。 因为 \(S_{\triangle ABD}=S_{\triangle BDC}+S_{\triangle ADC}=20\)， 所以 \(\frac{1}{2}×CD×2+\frac{1}{2}×CD×8 = 20\)， 所以 \(CD = 4\)，所以 \(\vert d + 3\vert = 4\)，所以 \(d = 1\) 或 \(d=-7\)， 所以点 \(D\) 的坐标为 \((0,1)\) 或 \((0,-7)\)。 

5 如图，在平面直角坐标系$xOy$中，函数$y = -x + b$的图象与函数$y=\frac{k}{x}(x ＜ 0)$的图象相交于点$A(-1,6)$，并与$x$轴交于点$C$.点$D$是线段$AC$上一点，$\triangle ODC$与$\triangle OAC$的面积比为$2:3$.
(1)$k =$ ，$b =$ ；
(2)求点$D$的坐标；
(3)若将$\triangle ODC$绕点$O$逆时针旋转，得到$\triangle OD'C'$，其中点$D'$落在$x$轴负半轴上，判断点$C'$是否落在函数$y=\frac{k}{x}(x ＜ 0)$的图象上，并说明理由.

答案：
5.
(1) \(-6\) \(5\) [解析]将 \(A(-1,6)\) 代入 \(y=-x + b\)，得 \(6 = 1 + b\)，所以 \(b = 5\)。 将 \(A(-1,6)\) 代入 \(y=\frac{k}{x}\)，得 \(6=\frac{k}{-1}\)，所以 \(k=-6\)。
(2) 如图，过点 \(D\) 作 \(DM\perp x\) 轴，垂足为 \(M\)，过点 \(A\) 作 \(AN\perp x\) 轴，垂足为 \(N\)。
因为 \(\frac{S_{\triangle ODC}}{S_{\triangle OAC}}=\frac{\frac{1}{2}OC\cdot DM}{\frac{1}{2}OC\cdot AN}=\frac{2}{3}\)，所以 \(\frac{DM}{AN}=\frac{2}{3}\)。 又点 \(A\) 的坐标为 \((-1,6)\)，所以 \(AN = 6\)， 所以 \(DM = 4\)，即点 \(D\) 的纵坐标为 \(4\)。 将 \(y = 4\) 代入 \(y=-x + 5\) 中，得 \(x = 1\)，所以 \(D(1,4)\)。
(3) 点 \(C'\) 不在函数 \(y=\frac{k}{x}\) 的图象上。理由如下： 由题意及
(2)可知，\(OD' = OD=\sqrt{OM^2+DM^2}=\sqrt{17}\)。 过点 \(C'\) 作 \(C'G\perp x\) 轴，垂足为 \(G\)，连接 \(OC'\)。 因为 \(S_{\triangle ODC}=S_{\triangle OD'C'}\)， 所以 \(OC\cdot DM=OD'\cdot C'G\)， 即 \(5×4=\sqrt{17}C'G\)，所以 \(C'G=\frac{20\sqrt{17}}{17}\)。 在 \(Rt\triangle OC'G\) 中， \(OG=\sqrt{OC'^2 - C'G^2}=\sqrt{25-\frac{400}{17}}=\frac{5\sqrt{17}}{17}\)， 所以点 \(C'\) 的坐标为 \((-\frac{5\sqrt{17}}{17},\frac{20\sqrt{17}}{17})\)。 因为 \((-\frac{5\sqrt{17}}{17})×\frac{20\sqrt{17}}{17}\neq - 6\)， 所以点 \(C'\) 不在函数 \(y=-\frac{6}{x}(x < 0)\) 的图象上。 

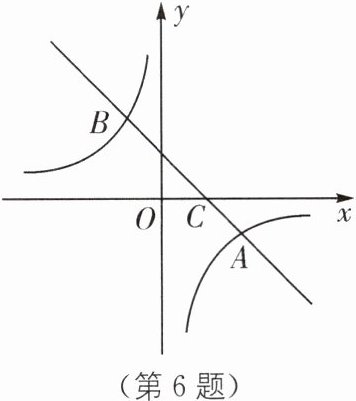
6 如图，在平面直角坐标系中，一次函数$y = k_1x + b$的图象与反比例函数$y=\frac{k_2}{x}$的图象交于$A(4,-2)$，$B(-2,n)$两点，与$x$轴交于点$C$.
(1)求$k_2$，$n$的值；
(2)请直接写出不等式$k_1x + b ＜\frac{k_2}{x}$的解集；
(3)将$x$轴下方的图象沿$x$轴翻折，点$A$落在点$A'$处，连接$A'B$，$A'C$，求$\triangle A'BC$的面积.

答案：  6.
(1) 将 \(A(4,-2)\) 代入 \(y=\frac{k_2}{x}\)，得 \(k_2=-8\)，所以 \(y=-\frac{8}{x}\)。 将 \((-2,n)\) 代入 \(y=-\frac{8}{x}\)，得 \(n = 4\)。故 \(k_2=-8\)，\(n = 4\)。
(2) 根据函数图象，可知 \(-2 < x < 0\) 或 \(x > 4\)。
(3) 将 \(A(4,-2)\)，\(B(-2,4)\) 代入 \(y = k_1x + b\)，得 \(k_1=-1\)，\(b = 2\)， 所以一次函数的解析式为 \(y=-x + 2\)，所以 \(C(2,0)\)。 由图象沿 \(x\) 轴翻折后，得 \(A'(4,2)\)。 \(S_{\triangle A'BC}=(4 + 2)×(4 + 2)×\frac{1}{2}-\frac{1}{2}×4×4-\frac{1}{2}×2×2 = 8\)。 故 \(\triangle A'BC\) 的面积为 \(8\)。