《2025年课时训练九年级数学下册人教版江苏人民出版社》

13. （2022·潍坊二模）如图，一段东西方向的海岸线MN上，小明从点A测得灯塔C位于北偏西15°方向，向东走300米到达点B处，测得灯塔C位于北偏西60°方向．
（1）求点A到灯塔C的距离AC的长（结果保留根号）；
（2）求灯塔C到海岸线MN的距离（结果保留根号）．

答案：
（1）如图，过点A作$AD\perp BC$，垂足为D。 由题意，得$\angle BAC = 90^{\circ}+15^{\circ}=105^{\circ}$，$AB = 300$米，$\angle ABC = 90^{\circ}-60^{\circ}=30^{\circ}$，所以$\angle ACB = 180^{\circ}-105^{\circ}-30^{\circ}=45^{\circ}$，$AD=\frac{1}{2}AB = 150$米。 在$Rt\triangle ADC$中，$\sin\angle ACD=\frac{AD}{AC}$，因为$AC=\frac{AD}{\sin45^{\circ}}=\frac{150}{\frac{\sqrt{2}}{2}} = 150\sqrt{2}$（米） 故点A到灯塔C的距离AC的长为$150\sqrt{2}$米。 （2）如图，过点C作$CE\perp MN$于点E，即灯塔C到海岸线MN的距离就是CE的长。 因为$\triangle ADC$为等腰直角三角形，所以$DC = AD = 150$米。 在$Rt\triangle ABD$中，$AD = 150$米，$AB = 300$米，所以$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{300^{2}-150^{2}} = 150\sqrt{3}$（米）， 所以$BC = BD + DC=(150\sqrt{3}+150)$米。 在$Rt\triangle BCE$中，$\angle ABC = 30^{\circ}$，所以$CE=\frac{1}{2}BC=(75\sqrt{3}+75)$米。 故灯塔C到海岸线MN的距离是$(75\sqrt{3}+75)$米。 方法技巧：解一般三角形、求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线。

14. （2023·天津一模）某大楼拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图，如图所示．按规定，地下停车库坡道上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE.（精确到0.1 m，参考数据：sin18°≈0.309 0，cos18°≈0.951 1，tan18°≈0.324 9）

答案： 在$Rt\triangle ABD$中，$\angle BAD = 18^{\circ}$，$AB = 9$m，所以$BD = AB\cdot\tan18^{\circ}\approx2.92$m，所以$CD = BD - BC = 2.92 - 0.5 = 2.42$（m）， 在$Rt\triangle CDE$中，$\angle CDE = 72^{\circ}$，$CD = 2.42$m，所以$\angle DCE = 18^{\circ}$，所以$CE = CD\cdot\cos18^{\circ}\approx2.3$m。 故CE的高为2.3 m。

15. （2022·安徽中考）如图，为了测量河对岸A，B两点间的距离，数学兴趣小组在河岸南侧选定观测点C，测得A，B均在C的北偏东37°方向上，沿正东方向行走90米至观测点D，测得A在D的正北方向，B在D的北偏西53°方向上．求A，B两点间的距离．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

答案：
如图，因为$CE// AD$，所以$\angle A=\angle ECA = 37^{\circ}$，所以$\angle CBD=\angle A+\angle ADB = 37^{\circ}+53^{\circ}=90^{\circ}$，所以$\angle ABD = 90^{\circ}$。 在$Rt\triangle BCD$中，$\angle BDC = 90^{\circ}-53^{\circ}=37^{\circ}$，$CD = 90$米，$\cos\angle BDC=\frac{BD}{CD}$，所以$BD = CD\cdot\cos37^{\circ}\approx90\times0.80 = 72$（米）。 在$Rt\triangle ABD$中，$\angle A = 37^{\circ}$，$BD = 72$米，$\tan A=\frac{BD}{AB}$，所以$AB=\frac{BD}{\tan37^{\circ}}\approx\frac{72}{0.75}=96$（米）。 故A，B两点间的距离约为96米。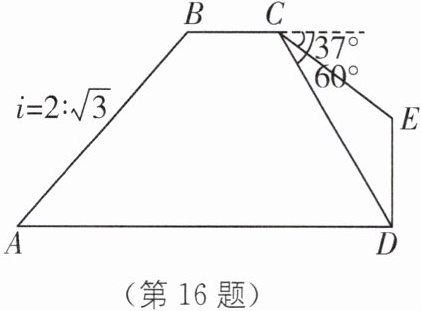关键提醒：本题考查了解直角三角形的应用——方向角问题。证明$\triangle CBD$和$\triangle ABD$是直角三角形是解题的关键。

16. [情境创新类问题]（2023·泸州中考）如图，某数学兴趣小组为了测量古树DE的高度，采用了如下的方法：先从与底端D同一水平线上的点A出发，沿坡度坡度为i = 2∶$\sqrt{3}$的斜坡AB前进20$\sqrt{7}$ m到达点B，沿水平方向前进前进一段距离后到达点C. 在点C处测得古树DE的顶端E的俯角为37°，底部D的俯角为60°，求古树DE的高度．（参考数据：sin37°≈$\frac{3}{5}$，cos37°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$，结果结果用根号表示，不取近似值）

答案：
如图，过点B作$BF\perp AD$，垂足为F，延长BC，DE交于点H。 在$Rt\triangle ABF$中，因为$i = 2:\sqrt{3}$，所以可设$BF = 2k$，$AF=\sqrt{3}k$。 因为$AB = 20\sqrt{7}$m，$BF^{2}+AF^{2}=AB^{2}$，所以$(2k)^{2}+(\sqrt{3}k)^{2}=(20\sqrt{7})^{2}$， 解得$k = 20$（负值舍去），所以$BF = 2k = 40$m。 因为BC是水平线，DE是铅直线，所以$DH\perp CH$，所以$\triangle CDH$和$\triangle CEH$都是直角三角形。 因为AD，BC都是水平线，$BF\perp AD$，$DH\perp BC$，所以四边形BFDH是矩形，所以$DH = BF = 40$m。 在$Rt\triangle CDH$中，因为$\tan\angle DCH=\frac{DH}{CH}$，所以$CH=\frac{DH}{\tan\angle DCH}=\frac{40}{\tan60^{\circ}}=\frac{40\sqrt{3}}{3}$（m）。 在$Rt\triangle CEH$中，因为$\tan\angle ECH=\frac{EH}{CH}$，所以$EH = CH\cdot\tan\angle ECH=\frac{40\sqrt{3}}{3}\cdot\tan37^{\circ}\approx\frac{40\sqrt{3}}{3}\times\frac{3}{4}=10\sqrt{3}$（m）， 所以$DE = DH - EH=(40 - 10\sqrt{3})$m。 故古树DE的高度为$(40 - 10\sqrt{3})$m。