第64页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
12(2023·宁德寿宁模拟)如图,在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$AB = 4$cm,$BC = 8$cm,在$\triangle ABC$的内部作一个矩形$DBFE$,其中$DB$,$BF$在两直角边上,设矩形的一边$BF = x$cm.
(1)$AD =$_______. $BD =$_______.
(2)设矩形$DBFE$的面积为$y$ $cm^{2}$,
①求$y$与$x$的解析式;
②当$x$取何值时,$y$的值最大? 最大值是多少?

(1)$AD =$_______. $BD =$_______.
(2)设矩形$DBFE$的面积为$y$ $cm^{2}$,
①求$y$与$x$的解析式;
②当$x$取何值时,$y$的值最大? 最大值是多少?

答案:
1)因为矩形\(DBFE\)在\(\triangle ABC\)内部,\(BF = x cm\),所以\(DE\parallel BC\),\(DE = BF = x cm\),\(\triangle ADE\sim\triangle ABC\)。在\(Rt\triangle ABC\)中,\(\angle B = 90^{\circ}\),\(AB = 4 cm\),\(BC = 8 cm\),则\(\frac{DE}{BC}=\frac{AD}{AB}\),即\(\frac{x}{8}=\frac{AD}{4}\),解得\(AD=\frac{x}{2}cm\),\(BD = AB - AD=(4 - \frac{x}{2})cm\)。 - (2)①\(y = BD\cdot BF=(4 - \frac{x}{2})x=-\frac{1}{2}x^{2}+4x\);②当\(x = \frac{-4}{2×(-\frac{1}{2})}=4\)时,\(y\)值最大为8。
13 在$\triangle ABC$中,$AB = 6$,$AC = 9$,点$D$在边$AB$所在的直线上,且$AD = 2$,过点$D$作$DE// BC$交边$AC$所在直线于点$E$,求$CE$的长.
答案:
- 当点D在边AB上时,\(AB = 6\),\(AC = 9\),\(AD = 2\),则\(BD = AB - AD = 4\)。因为\(DE\parallel BC\),所以\(\frac{BD}{AB}=\frac{CE}{AC}\),即\(\frac{4}{6}=\frac{CE}{9}\),解得\(CE = 6\)。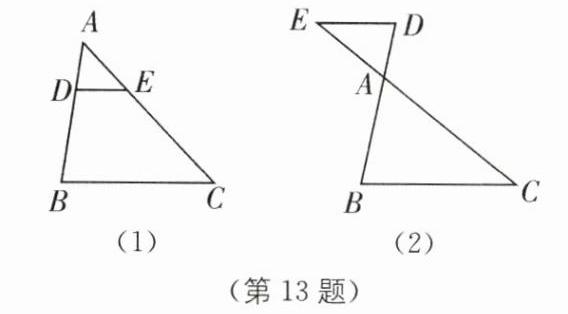
- 当点D在边BA的延长线上时,\(AB = 6\),\(AC = 9\),\(AD = 2\),则\(BD = AB + AD = 8\)。因为\(DE\parallel BC\),所以\(\frac{BD}{AB}=\frac{CE}{AC}\),即\(\frac{8}{6}=\frac{CE}{9}\),解得\(CE = 12\)。所以\(CE\)长为6或12。
- 当点D在边AB上时,\(AB = 6\),\(AC = 9\),\(AD = 2\),则\(BD = AB - AD = 4\)。因为\(DE\parallel BC\),所以\(\frac{BD}{AB}=\frac{CE}{AC}\),即\(\frac{4}{6}=\frac{CE}{9}\),解得\(CE = 6\)。

- 当点D在边BA的延长线上时,\(AB = 6\),\(AC = 9\),\(AD = 2\),则\(BD = AB + AD = 8\)。因为\(DE\parallel BC\),所以\(\frac{BD}{AB}=\frac{CE}{AC}\),即\(\frac{8}{6}=\frac{CE}{9}\),解得\(CE = 12\)。所以\(CE\)长为6或12。
14 (1)如图(1),在$\triangle ABC$中,点$D$,$E$,$Q$分别在$AB$,$AC$,$BC$上,且$DE// BC$,$AQ$交$DE$于点$P$. 求证:$\frac{DP}{BQ}=\frac{PE}{QC}$.
(2)如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,正方形$DEFG$的四个顶点在$\triangle ABC$的边上,连接$AG$,$AF$分别交$DE$于$M$,$N$两点.
①如图(2),若$AB = AC = 1$,直接写出$MN$的长;
②如图(3),求证:$MN^{2}=DM\cdot EN$.

(2)如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,正方形$DEFG$的四个顶点在$\triangle ABC$的边上,连接$AG$,$AF$分别交$DE$于$M$,$N$两点.
①如图(2),若$AB = AC = 1$,直接写出$MN$的长;
②如图(3),求证:$MN^{2}=DM\cdot EN$.

答案:
1)因为\(DP\parallel BQ\),所以\(\triangle ADP\sim\triangle ABQ\),\(\frac{DP}{BQ}=\frac{AP}{AQ}\),同理\(\frac{PE}{QC}=\frac{AP}{AQ}\),所以\(\frac{DP}{BQ}=\frac{PE}{QC}\)。 - (2)①答案为\(\frac{\sqrt{2}}{9}\);②因为\(\angle B+\angle C = 90^{\circ}\),\(\angle CEF+\angle C = 90^{\circ}\),所以\(\angle B=\angle CEF\),又\(\angle BGD=\angle EFC\),所以\(\triangle BGD\sim\triangle EFC\),\(\frac{DG}{CF}=\frac{BG}{EF}\),\(DG\cdot EF = CF\cdot BG\)。又\(DG = GF = EF\),所以\(GF^{2}=CF\cdot BG\)。由(1)结论可得\(\frac{DM}{BG}=\frac{MN}{GF}=\frac{EN}{CF}\),所以\((\frac{MN}{GF})^{2}=\frac{DM}{BG}\cdot\frac{EN}{CF}\),即\(MN^{2}=DM\cdot EN\)。
查看更多完整答案,请扫码查看


