2025年经纶学典学霸黑白题高中数学必修第一册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年经纶学典学霸黑白题高中数学必修第一册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. (多选)(2025·河北张家口高一期中)下列函数中,既是偶函数又在区间$(0, +\infty)$上单调递减的是(
A.$y = \frac{1}{|x|}$
B.$y = x^2 + 2$
C.$y = x - \frac{1}{x}$
D.$y = 2 - |x|$
AD
)A.$y = \frac{1}{|x|}$
B.$y = x^2 + 2$
C.$y = x - \frac{1}{x}$
D.$y = 2 - |x|$
答案:
1. AD 解析:A 选项,$f(x)=\frac{1}{|x|}$定义域为$(-\infty,0)\cup(0,+\infty)$,且$f(-x)=\frac{1}{|-x|}=\frac{1}{|x|}=f(x)$,故$y=\frac{1}{|x|}$为偶函数,且$x>0$时,$y=\frac{1}{x}$,满足在$(0,+\infty)$上单调递减,A 正确;B 选项,$y=x^{2}+2$在$(0,+\infty)$上单调递增,B 错误;C 选项,$g(x)=x-\frac{1}{x}$定义域为$(-\infty,0)\cup(0,+\infty)$,且$g(-x)=-x+\frac{1}{x}=-g(x)$,故$y=x-\frac{1}{x}$是奇函数,C 错误;D 选项,函数$h(x)=2-|x|$定义域为$\mathbf{R}$,且$h(-x)=2-|-x|=2-|x|=h(x)$,故$y=2-|x|$为偶函数,且$x>0$时,$y=2-x$,其在$(0,+\infty)$上单调递减,D 正确。故选 AD。
2. (2025·浙江嘉兴高一月考)若函数$y = f(x)$是定义在$\mathbf{R}$上的奇函数,则$f(-1) + f(0) + f(1) =$(
A.$0$
B.$1$
C.$-2$
D.$-3$
A
)A.$0$
B.$1$
C.$-2$
D.$-3$
答案:
2. A 解析:因为函数$y = f(x)$是定义在$\mathbf{R}$上的奇函数,所以$f(0)=0$,$f(-1)+f(1)=0$,所以$f(-1)+f(0)+f(1)=0$。故选 A。
3. 定义在$\mathbf{R}$上的函数$f(x)$,若$g(x) = f(|x|) - |f(x)|$,有下列两个结论:①若$f(x)$是偶函数,则$g(x)$是奇函数;②若$f(x)$是偶函数,则$g(x)$是偶函数,则(
A.①②均正确
B.①②均错误
C.①正确②错误
D.①错误②正确
D
)A.①②均正确
B.①②均错误
C.①正确②错误
D.①错误②正确
答案:
3. D 解析:对于①,$f(x)$是偶函数时,有$f(-x)=f(x)$,则$g(-x)=f(|-x|)-|f(-x)|=f(|x|)-|f(x)|=g(x)$,$g(x)$是偶函数,故①错误,②正确。故选 D。
4. (2025·四川遂宁高一期中)已知定义域为$[-4, 4]$的奇函数$f(x)$在$(0, 4]$上的图象如图所示,则下列说法错误的是(
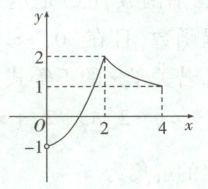
A.$f(-4) = -1$
B.$f(0) = 0$
C.$f(x)$在定义域上不存在最小值
D.$f(x)$在$[-4, 4]$的最大值与最小值之和为$0$
C
)
A.$f(-4) = -1$
B.$f(0) = 0$
C.$f(x)$在定义域上不存在最小值
D.$f(x)$在$[-4, 4]$的最大值与最小值之和为$0$
答案:
4. C 解析:对于 A,由$f(x)$为定义域为$[-4,4]$的奇函数,则图象关于点$(0,0)$对称,$f(x)+f(-x)=0$,由题图知$f(4)=1$,则$f(-4)=-1$,故 A 正确;对于 B,$0\in[-4,4]$,$f(x)$为奇函数,则$f(0)=0$,故 B 正确;对于 C,由题图知$f(x)$在$(0,4]$上的最大值为$f(2)=2$,则$f(x)$在$[-4,0)$上的最小值为$f(-2)=-2$,因此可得$f(x)$在定义域$[-4,4]$上存在最小值为$-2$,故 C 错误;对于 D,由$f(x)$在$[-4,4]$上的最大值为 2,最小值为$-2$,则最大值与最小值之和为 0,故 D 正确。故选 C。
5. (2025·山东淄博高一期中)若函数$y = f(x)$为偶函数,且在$(0, +\infty)$上是减函数,又$f(3) = 0$,则不等式$\frac{f(x) + f(-x)}{2x} < 0$的解集为(
A.$(-3, 3)$
B.$(-\infty, -3) \cup (3, +\infty)$
C.$(-\infty, -3) \cup (0, 3)$
D.$(-3, 0) \cup (3, +\infty)$
D
)A.$(-3, 3)$
B.$(-\infty, -3) \cup (3, +\infty)$
C.$(-\infty, -3) \cup (0, 3)$
D.$(-3, 0) \cup (3, +\infty)$
答案:
5. D 解析:$\because f(x)$为偶函数,$\therefore f(-x)=f(x)$,$\therefore\frac{f(x)+f(-x)}{2x}<0$可转化为$\frac{f(x)}{x}<0$,而$f(x)$在$(0,+\infty)$上是减函数,且$f(3)=0$,故当$x>3$时,$f(x)<0$,当$-3<x<0$时,$f(x)>0$,故$\frac{f(x)}{x}<0$的解集为$(-3,0)\cup(3,+\infty)$。故选 D。
6. 已知函数$f(x)$是奇函数,$g(x)$是偶函数,且$f(x) + g(x) = 3x + \frac{2}{x - 2}$,则$f(x) =$(
A.$6x - \frac{4x}{x^2 - 4}$
B.$6x + \frac{4x}{x^2 - 4}$
C.$3x - \frac{3x}{x^2 - 4}$
D.$3x + \frac{2x}{x^2 - 4}$
D
)A.$6x - \frac{4x}{x^2 - 4}$
B.$6x + \frac{4x}{x^2 - 4}$
C.$3x - \frac{3x}{x^2 - 4}$
D.$3x + \frac{2x}{x^2 - 4}$
答案:
6. D 解析:因为$f(x)$是奇函数,$g(x)$是偶函数,所以$f(-x)= -f(x)$,$g(-x)=g(x)$,所以$\begin{cases}f(x)+g(x)=3x+\frac{2}{x - 2}\\-f(x)+g(x)=-3x - \frac{2}{x + 2}\end{cases}$,即$\begin{cases}f(x)+g(x)=3x+\frac{2}{x - 2}\\f(-x)+g(-x)=-3x - \frac{2}{-x - 2}\end{cases}$,因此$f(x)=3x+\frac{2x}{x^{2}-4}$。故选 D。
7. (多选)(2025·山东枣庄高一期中)已知函数$y = f(x)$是定义在$\mathbf{R}$上的偶函数,当$x \leq 0$时,$f(x) = x(x + 1)$,则下列说法正确的是(
A.函数$f(x)$有$3$个单调区间
B.当$x > 0$时,$f(x) = x(x - 1)$
C.函数$f(x)$有最小值$-\frac{1}{4}$
D.不等式$f(x) < 0$的解集是$(-1, 1)$
BC
)A.函数$f(x)$有$3$个单调区间
B.当$x > 0$时,$f(x) = x(x - 1)$
C.函数$f(x)$有最小值$-\frac{1}{4}$
D.不等式$f(x) < 0$的解集是$(-1, 1)$
答案:
7. BC 解析:当$x>0$时,$-x<0$,因为$x\leq0$时,$f(x)=x(x + 1)$,所以$f(-x)=-x(-x + 1)$。又因为$y = f(x)$是定义在$\mathbf{R}$上的偶函数,所以$x>0$时,$f(x)=-x(-x + 1)=x^{2}-x$,即$f(x)=\begin{cases}x^{2}-x(x>0)\\x^{2}+x(x\leq0)\end{cases}$,如图所示:

对 A,由图知,函数$f(x)$有 4 个单调区间,故 A 错误;对 B,由上述分析知,当$x>0$时,$f(x)=x^{2}-x$,故 B 正确;对 C,由图知,当$x=-\frac{1}{2×1}=-\frac{1}{2}$或$x=\frac{-1}{2×1}=\frac{1}{2}$时,函数$f(x)$取得最小值$f(x)_{\min}=f(-\frac{1}{2})=f(\frac{1}{2})=-\frac{1}{4}$,故 C 正确;对 D,由图知,不等式$f(x)<0$的解集是$(-1,0)\cup(0,1)$,故 D 错误。故选 BC。
7. BC 解析:当$x>0$时,$-x<0$,因为$x\leq0$时,$f(x)=x(x + 1)$,所以$f(-x)=-x(-x + 1)$。又因为$y = f(x)$是定义在$\mathbf{R}$上的偶函数,所以$x>0$时,$f(x)=-x(-x + 1)=x^{2}-x$,即$f(x)=\begin{cases}x^{2}-x(x>0)\\x^{2}+x(x\leq0)\end{cases}$,如图所示:

对 A,由图知,函数$f(x)$有 4 个单调区间,故 A 错误;对 B,由上述分析知,当$x>0$时,$f(x)=x^{2}-x$,故 B 正确;对 C,由图知,当$x=-\frac{1}{2×1}=-\frac{1}{2}$或$x=\frac{-1}{2×1}=\frac{1}{2}$时,函数$f(x)$取得最小值$f(x)_{\min}=f(-\frac{1}{2})=f(\frac{1}{2})=-\frac{1}{4}$,故 C 正确;对 D,由图知,不等式$f(x)<0$的解集是$(-1,0)\cup(0,1)$,故 D 错误。故选 BC。
8. (2025·江苏苏州中学高一期中)已知$f(x)$是定义在$\mathbf{R}$上的奇函数,当$x > 0$时,$f(x) = \sqrt{x} + 2$,则不等式$f(x) > x$的解集为(
A.$(-\infty, -4) \cup (0, 4)$
B.$(-4, 0) \cup (4, +\infty)$
C.$(-4, 0) \cup (0, 4)$
D.$(-\infty, -4) \cup (4, +\infty)$
A
)A.$(-\infty, -4) \cup (0, 4)$
B.$(-4, 0) \cup (4, +\infty)$
C.$(-4, 0) \cup (0, 4)$
D.$(-\infty, -4) \cup (4, +\infty)$
答案:
8. A 解析:函数$f(x)$是定义在$\mathbf{R}$上的奇函数,由当$x>0$时,$f(x)=\sqrt{x}+2$,得当$x<0$时,$f(x)=-f(-x)=-(\sqrt{-x}+2)=-\sqrt{-x}-2$,$f(0)=0$。当$x>0$时,$f(x)>x\Leftrightarrow\sqrt{x}+2>x\Leftrightarrow(\sqrt{x}-2)(\sqrt{x}+1)<0$,解得$0<x<4$;当$x<0$时,$f(x)>x\Leftrightarrow-\sqrt{-x}-2>x\Leftrightarrow(\sqrt{-x}-2)(\sqrt{-x}+1)>0$,解得$x<-4$;当$x=0$时,$f(x)>x$无解,所以不等式$f(x)>x$的解集为$(-\infty,-4)\cup(0,4)$。故选 A。
查看更多完整答案,请扫码查看


