2025年经纶学典学霸黑白题高中数学必修第一册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年经纶学典学霸黑白题高中数学必修第一册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. * (全国高考)设$a\log_{3}4 = 2$,则$4^{-a}=$(
A.$\frac{1}{16}$
B.$\frac{1}{9}$
C.$\frac{1}{8}$
D.$\frac{1}{6}$
B
)A.$\frac{1}{16}$
B.$\frac{1}{9}$
C.$\frac{1}{8}$
D.$\frac{1}{6}$
答案:
1.B 解析:由$a\log_3{4}=2$可得$\log_3{4^a}=2,$所以4^a=9,所以$4^{-a}=\frac{1}{9}.$故选B。
2. * (2022·天津)化简$(2\log_{4}3 + \log_{8}3)·(\log_{3}2 + \log_{9}2)=$(
A.$1$
B.$\frac{5}{4}$
C.$2$
D.$\frac{5}{2}$
C
)A.$1$
B.$\frac{5}{4}$
C.$2$
D.$\frac{5}{2}$
答案:
2.C 解析:原式$=(2×\frac{1}{2}\log_2{3}+\frac{1}{3}\log_3{3})(\log_3{2}+\frac{1}{2}\log_3{2})=$
$\frac{4}{3}\log_2{3}×\frac{3}{2}\log_3{2}=2.$故选C。
$\frac{4}{3}\log_2{3}×\frac{3}{2}\log_3{2}=2.$故选C。
3. * (2022·浙江)已知$2^{a}=5$,$\log_{8}3 = b$,则$4^{a - 3b}=$(
A.$25$
B.$5$
C.$\frac{25}{9}$
D.$\frac{5}{3}$
C
)A.$25$
B.$5$
C.$\frac{25}{9}$
D.$\frac{5}{3}$
答案:
3.C 解析:因为$2^a=5,b=\log_8{3}=\frac{1}{3}\log_2{3},$即$2^{3b}=3,$所以
$4^{a - 3b}=\frac{4^a}{(2^a)^2·3^2}=\frac{25}{9×3^2}=\frac{25}{9}.$故选C.
$4^{a - 3b}=\frac{4^a}{(2^a)^2·3^2}=\frac{25}{9×3^2}=\frac{25}{9}.$故选C.
4. * (天津高考)若$2^{a}=5^{b}=10$,则$\frac{1}{a}+\frac{1}{b}=$(
A.$-1$
B.$\lg7$
C.$1$
D.$\log_{7}10$
C
)A.$-1$
B.$\lg7$
C.$1$
D.$\log_{7}10$
答案:
4.C 解析:$\because2^a=5^b=10,\therefore a=\log_2{10},b=\log_5{10},\therefore\frac{1}{a}+\frac{1}{b}=$
$\frac{1}{\log_2{10}}+\frac{1}{\log_5{10}}=\lg2+\lg5=\lg10=1.$故选C.
$\frac{1}{\log_2{10}}+\frac{1}{\log_5{10}}=\lg2+\lg5=\lg10=1.$故选C.
5. * (湖南高考)若$a\gt0$,$a^{\frac{2}{3}}=\frac{4}{9}$,则$\log_{\frac{2}{3}}a=$
3
.
答案:
5.3 解析:$\becausea^{\frac{2}{3}}=\frac{4}{9},\therefore$两边同时取$\frac{3}{2}$次方得$a=(\frac{4}{9})^{\frac{3}{2}}=$
$(\frac{2}{3})^3,\therefore\log_2{a}=\log_2{(\frac{2}{3})^3}=3.$故答案为3.
$(\frac{2}{3})^3,\therefore\log_2{a}=\log_2{(\frac{2}{3})^3}=3.$故答案为3.
6. * (安徽高考)$\left(\frac{16}{81}\right)^{-\frac{3}{4}}+\log_{3}\frac{5}{4}+\log_{3}\frac{4}{5}=$
$\frac{27}{8}$
.
答案:
$6.\frac{27}{8} $解析:原式$=[(\frac{2}{3})^4]^{\frac{3}{4}}+\log_3{(\frac{5}{4}×\frac{4}{5})}=\frac{27}{8}+$
$\log_3{1}=\frac{27}{8}.$故答案为$\frac{27}{8}.$
$\log_3{1}=\frac{27}{8}.$故答案为$\frac{27}{8}.$
7. * (重庆高考)若$x\gt0$,则$\left(2x^{\frac{1}{4}} + 3^{\frac{3}{2}}\right)\left(2x^{\frac{1}{4}} - 3^{\frac{3}{2}}\right)-4x^{-\frac{1}{2}}\left(x - x^{\frac{1}{2}}\right)=$
-23
.
答案:
7.-23 解析:原式$=(2x^{\frac{1}{4}})^2-(3^{\frac{3}{2}})^2-4x^{\frac{1}{2}}· x+4x^{\frac{1}{2}}· x^{\frac{1}{2}}=$
$4x^{\frac{1}{2}}-3^3-4x^{\frac{1}{2}+1}+4x^{\frac{1}{12}}=4 - 27=-23.$故答案为-23.
$4x^{\frac{1}{2}}-3^3-4x^{\frac{1}{2}+1}+4x^{\frac{1}{12}}=4 - 27=-23.$故答案为-23.
8. * (2024·全国甲理)已知$a\gt1$且$\frac{1}{\log_{8}a}-\frac{1}{\log_{a}4}=-\frac{5}{2}$,则$a=$
64
.
答案:
8.64 解析:由题$\frac{1}{\log_8{a}}+\frac{1}{\log_4{a}}=\frac{3}{2}\log_2{a}=-\frac{5}{2},$整理得
$(\log_2{a})^2-5\log_2{a}-6=0\Rightarrow\log_2{a}=-1$或$\log_2{a}=6,$又a>1,所以
$\log_2{a=6}=\log_2{2^6},$故$a=2^6=64.$故答案为64.
$(\log_2{a})^2-5\log_2{a}-6=0\Rightarrow\log_2{a}=-1$或$\log_2{a}=6,$又a>1,所以
$\log_2{a=6}=\log_2{2^6},$故$a=2^6=64.$故答案为64.
9. * (天津高考)已知$\log_{2}a + \log_{2}b\geq1$,则$3^{a}+9^{b}$的最小值为
18
.
答案:
9.18 解析:由$\log_2{a}+\log_2{b}\geq1$得$ab\geq2,$且a>0,b>0.又3^a+
$9^b=3^a+3^{2b}\geq2\sqrt{3^a·3^{2b}}=2\sqrt{3^{a + 2b}}.$因为$a + 2b\geq2\sqrt{2ab}\geq$
$2\sqrt{2×2}=4($当且仅当a=2b时取等号),所以$3^a+9^b\geq$
$2\sqrt{3^4}=18.$即3^a+9^b的最小值为18.故答案为18.
$9^b=3^a+3^{2b}\geq2\sqrt{3^a·3^{2b}}=2\sqrt{3^{a + 2b}}.$因为$a + 2b\geq2\sqrt{2ab}\geq$
$2\sqrt{2×2}=4($当且仅当a=2b时取等号),所以$3^a+9^b\geq$
$2\sqrt{3^4}=18.$即3^a+9^b的最小值为18.故答案为18.
10. * (2024·北京)生物丰富度指数$d = \frac{S - 1}{\ln\frac{1}{N}}$是河流水质的一个评价指标,其中$S$,$N$分别表示河流中的生物种类数与生物个体总数.生物丰富度指数$d$越大,水质越好.如果某河流治理前后的生物种类数$S$没有变化,生物个体总数由$N_{1}$变为$N_{2}$,生物丰富度指数由$2.1$提高到$3.15$,则(
A.$3N_{2}=2N_{1}$
B.$2N_{2}=3N_{1}$
C.$N_{2}^{2}=N_{1}^{3}$
D.$N_{2}^{3}=N_{1}^{2}$
D
)A.$3N_{2}=2N_{1}$
B.$2N_{2}=3N_{1}$
C.$N_{2}^{2}=N_{1}^{3}$
D.$N_{2}^{3}=N_{1}^{2}$
答案:
10.D 解析:由题意得$\frac{S - 1}{\ln N_1}=2.1,\frac{S - 1}{\ln N_2}=3.15,$则$2.1\ln N_1=$
$3.15\ln N_2,$即$2\ln N_1=3\ln N_2,$所以$N_2^3=N_1^2.$故选D.
$3.15\ln N_2,$即$2\ln N_1=3\ln N_2,$所以$N_2^3=N_1^2.$故选D.
11. * (北京高考)根据有关资料,围棋状态空间复杂度的上限$M$约为$3^{361}$,而可观测宇宙中普通物质的原子总数$N$约为$10^{80}$.则下列各数中与$\frac{M}{N}$最接近的是(参考数据:$\lg3\approx0.48$)(
A.$10^{33}$
B.$10^{53}$
C.$10^{73}$
D.$10^{93}$
D
)A.$10^{33}$
B.$10^{53}$
C.$10^{73}$
D.$10^{93}$
答案:
11.D 解析:设$\frac{M}{N}=x=\frac{3^{361}}{10^{80}},$两边取对数,$\lg x=\lg\frac{3^{361}}{10^{80}}=\lg3^{361}-$
$\lg10^{80}=361×\lg3-80\approx93.28,$所以$x=10^{93.28},$即$\frac{M}{N}$最接近
$10^{93}.$故选D.
$\lg10^{80}=361×\lg3-80\approx93.28,$所以$x=10^{93.28},$即$\frac{M}{N}$最接近
$10^{93}.$故选D.
12. * (2022·北京)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与$T$和$\lg P$的关系,其中$T$表示温度,单位是$K$;$P$表示压强,单位是$bar$.下列结论中正确的是(
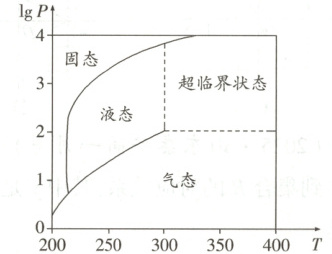
A.当$T = 220$,$P = 1026$时,二氧化碳处于液态
B.当$T = 270$,$P = 128$时,二氧化碳处于气态
C.当$T = 300$,$P = 9987$时,二氧化碳处于超临界状态
D.当$T = 360$,$P = 729$时,二氧化碳处于超临界状态
D
)
A.当$T = 220$,$P = 1026$时,二氧化碳处于液态
B.当$T = 270$,$P = 128$时,二氧化碳处于气态
C.当$T = 300$,$P = 9987$时,二氧化碳处于超临界状态
D.当$T = 360$,$P = 729$时,二氧化碳处于超临界状态
答案:
12.D 解析:当T=220,P=1026时,$\lg P>3,$此时二氧化碳处
于固态,故A错误;当T=270,P=128时,2<\lg P<3,此时二
氧化碳处于液态,故B错误;当T=300,P=9987时,$\lg P$与
4非常接近,故此时二氧化碳处于固态,故C错误;当T=
360,P=729时,2<\lg P<3,故此时二氧化碳处于超临界状
态,故D正确.故选D.
于固态,故A错误;当T=270,P=128时,2<\lg P<3,此时二
氧化碳处于液态,故B错误;当T=300,P=9987时,$\lg P$与
4非常接近,故此时二氧化碳处于固态,故C错误;当T=
360,P=729时,2<\lg P<3,故此时二氧化碳处于超临界状
态,故D正确.故选D.
查看更多完整答案,请扫码查看


