2025年经纶学典学霸黑白题高中数学必修第一册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年经纶学典学霸黑白题高中数学必修第一册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第121页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. (2025·江苏常州高一期末)为了得到函数$ y = \sin\left(2x + \frac{\pi}{6}\right) $的图象,可以将函数$ y = \cos 2x $的图象 (
A.向右平移$\frac{\pi}{6}$个单位长度
B.向右平移$\frac{\pi}{3}$个单位长度
C.向左平移$\frac{\pi}{6}$个单位长度
D.向左平移$\frac{\pi}{3}$个单位长度
A
)A.向右平移$\frac{\pi}{6}$个单位长度
B.向右平移$\frac{\pi}{3}$个单位长度
C.向左平移$\frac{\pi}{6}$个单位长度
D.向左平移$\frac{\pi}{3}$个单位长度
答案:
1.A解析:$y = \sin \left( 2x + \frac {\pi}{6} \right) = \cos \left( \frac {\pi}{2} - 2x - \frac {\pi}{6} \right) = \cos \left( \frac {\pi}{3} - 2x \right) = \cos \left( 2x - \frac {\pi}{3} \right)$,设$x \to x + \varphi$,$y = \cos 2(x + \varphi) = \cos (2x + 2\varphi)$,令$2\varphi = - \frac {\pi}{3}$,$\varphi = - \frac {\pi}{6}$,把函数$y = \cos 2x$的图象向右平移$\frac {\pi}{6}$个单位长度得到函数$y = \sin \left( 2x + \frac {\pi}{6} \right)$的图象。故选A。
2. 如图是周期为$\pi$的函数$ y = \cos(\omega x + \varphi) $ ($\omega > 0, 0 < \varphi < \pi$)的部分图象,则$\varphi =$ (
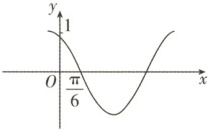
A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{2\pi}{3}$
D.$\frac{5\pi}{6}$
A
)
A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{2\pi}{3}$
D.$\frac{5\pi}{6}$
答案:
2.A解析:由周期$T = \frac {2\pi}{\omega} = \pi$,得$\omega = 2$,由五点对应法得$2 × \frac {\pi}{6} + \varphi = \frac {\pi}{2}$,得$\varphi = \frac {\pi}{6}$。故选A。
3. * (多选)(2025·山西太原高一期末)已知函数$ f(x) = \sin 2x $,$ g(x) = \tan 2x $,则下列结论正确的是 (
A.$ f(x) $,$ g(x) $的最小正周期都是$\pi$
B.$ f(x) $,$ g(x) $都是奇函数
C.$ f(x) $,$ g(x) $在$\left(-\frac{\pi}{4}, \frac{\pi}{4}\right)$上都单调递增
D.$ f(x) $,$ g(x) $的对称中心相同
BC
)A.$ f(x) $,$ g(x) $的最小正周期都是$\pi$
B.$ f(x) $,$ g(x) $都是奇函数
C.$ f(x) $,$ g(x) $在$\left(-\frac{\pi}{4}, \frac{\pi}{4}\right)$上都单调递增
D.$ f(x) $,$ g(x) $的对称中心相同
答案:
3.BC解析:对于A,易知$g(x) = \tan 2x$的最小正周期是$\frac {\pi}{2}$,即A错误;对于B,易知$f(-x) = \sin(-2x) = - \sin 2x = -f(x)$,$g(-x) = \tan(-2x) = -\tan 2x = -g(x)$,且$f(x)$,$g(x)$的定义域都为$\mathbf {R}$,满足奇函数定义,因此它们都是奇函数,可得B正确;对于C,当$x \in \left( - \frac {\pi}{4},\frac {\pi}{4} \right)$时,$2x \in \left( - \frac {\pi}{2},\frac {\pi}{2} \right)$,再由正弦函数和正切函数单调性可得C正确;对于D,$f(x)$的对称中心的横坐标满足$2x = k\pi$,$k \in \mathbf {Z}$,即$x = \frac {k}{2}\pi$,$k \in \mathbf {Z}$,可得$f(x)$的对称中心为$\left( \frac {k}{2}\pi,0 \right)$,$k \in \mathbf {Z}$,而对于$g(x) = \tan 2x$,其对称中心的横坐标满足$2x = \frac {k}{2}\pi$,$k \in \mathbf {Z}$,可得$x = \frac {k}{4}\pi$,$k \in \mathbf {Z}$,即$g(x)$的对称中心为$\left( \frac {k}{4}\pi,0 \right)$,$k \in \mathbf {Z}$,因此$f(x)$,$g(x)$的对称中心不完全相同,故D错误。故选BC。
4. * (多选)下列不等式中一定成立的是 (
A.$ \sin 470° > \sin 115° $
B.$ \cos \frac{16\pi}{7} > \cos \frac{17\pi}{8} $
C.$ \cos 226° > \sin 224° $
D.$ \tan 1600° > \tan 1415° $
AD
)A.$ \sin 470° > \sin 115° $
B.$ \cos \frac{16\pi}{7} > \cos \frac{17\pi}{8} $
C.$ \cos 226° > \sin 224° $
D.$ \tan 1600° > \tan 1415° $
答案:
4.AD解析:$\sin 470° = \sin 110° > \sin 115°$,故A正确;因为$\cos \frac {16\pi}{7} = \cos \frac {2\pi}{7}$,$\cos \frac {17\pi}{8} = \cos \frac {\pi}{8}$,又$\frac {2\pi}{7} > \frac {\pi}{8}$,所以$\cos \frac {2\pi}{7} < \cos \frac {\pi}{8}$,故B错误;因为$\cos 226° = \cos (180° + 46°) = -\cos 46° = -\cos (90° - 44°) = -\sin 44°$,$\sin 224° = \sin (180° + 44°) = -\sin 44°$,所以$\cos 226° = \sin 224°$,故C错误;因为$\tan 1600° = \tan (4 × 360° + 160°) = \tan 160° = \tan (180° - 20°) = -\tan 20°$,$\tan 1415° = \tan (4 × 360° - 25°) = -\tan 25°$,又$\tan 25° > \tan 20°$,所以$-\tan 25° < -\tan 20°$,故D正确。故选AD。
5. * (2025·黑龙江哈尔滨高一期末)已知函数$ f(x) = \left(\frac{1}{2}a - \frac{3}{2}\right)\cos x + \left(\frac{\sqrt{3}}{2}a + \frac{\sqrt{3}}{2}\right)\sin x $是偶函数.若将曲线$ y = f(2x) $向左平移$\frac{\pi}{8}$个单位长度后,得到曲线$ y = g(x) $,则函数$ y = g(x) $的单调递增区间是 (
A.$\left[k\pi - \frac{7\pi}{12}, k\pi - \frac{\pi}{12}\right](k \in \mathbf{Z})$
B.$\left[k\pi - \frac{\pi}{12}, k\pi + \frac{5\pi}{12}\right](k \in \mathbf{Z})$
C.$\left[k\pi - \frac{\pi}{8}, k\pi + \frac{3\pi}{8}\right](k \in \mathbf{Z})$
D.$\left[k\pi - \frac{\pi}{4}, k\pi + \frac{3\pi}{4}\right](k \in \mathbf{Z})$
C
)A.$\left[k\pi - \frac{7\pi}{12}, k\pi - \frac{\pi}{12}\right](k \in \mathbf{Z})$
B.$\left[k\pi - \frac{\pi}{12}, k\pi + \frac{5\pi}{12}\right](k \in \mathbf{Z})$
C.$\left[k\pi - \frac{\pi}{8}, k\pi + \frac{3\pi}{8}\right](k \in \mathbf{Z})$
D.$\left[k\pi - \frac{\pi}{4}, k\pi + \frac{3\pi}{4}\right](k \in \mathbf{Z})$
答案:
5.C解析:因为$f(x) = \left( \frac {1}{2}a - \frac {3}{2} \right) \cos x + \left( \frac {\sqrt {3}}{2}a + \frac {\sqrt {3}}{2} \right) \sin x$为偶函数,所以$f(-x) = f(x)$,即$\left( \frac {1}{2}a - \frac {3}{2} \right) \cos x + \left( \frac {\sqrt {3}}{2}a + \frac {\sqrt {3}}{2} \right) \sin x = \left( \frac {1}{2}a - \frac {3}{2} \right) \cos x - \left( \frac {\sqrt {3}}{2}a + \frac {\sqrt {3}}{2} \right) \sin x$,所以$\frac {\sqrt {3}}{2}a + \frac {\sqrt {3}}{2} = 0$,解得$a = -1$,所以$f(x) = -2 \cos x$。将曲线$y = f(2x)$向左平移$\frac {\pi}{8}$个单位长度后,得到曲线$g(x) = -2 \cos 2 \left( x + \frac {\pi}{8} \right) = -2 \cos \left( 2x + \frac {\pi}{4} \right)$,函数$y = 2 \cos \left( 2x + \frac {\pi}{4} \right)$的减区间即为函数$g(x)$的增区间。$2k\pi \leqslant 2x + \frac {\pi}{4} \leqslant 2k\pi + \pi$,$k \in \mathbf {Z}$,所以$2k\pi - \frac {\pi}{4} \leqslant 2x \leqslant 2k\pi + \pi - \frac {\pi}{4}$,$k \in \mathbf {Z}$,即$k\pi - \frac {\pi}{8} \leqslant x \leqslant k\pi + \frac {3\pi}{8}$,$k \in \mathbf {Z}$,所以函数$g(x)$的增区间为$\left[ k\pi - \frac {\pi}{8},k\pi + \frac {3\pi}{8} \right] (k \in \mathbf {Z})$。故选C。
6. * (多选)(2025·吉林通化高一月考)已知函数$ f(x) = \cos(\omega x + \varphi) + 1 $(其中$\omega$,$\varphi$均为常数,且$\omega > 0$,$|\varphi| < \pi$)恰能满足下列4个条件中的3个:
①函数$ f(x) $的最小正周期为$\pi$;
②函数$ f(x) $的图象经过点$\left(0, \frac{3}{2}\right)$;
③函数$ f(x) $的图象关于点$\left(\frac{5\pi}{12}, 1\right)$对称;
④函数$ f(x) $的图象关于直线$ x = -\frac{\pi}{6} $对称.
则这3个条件的序号可以是 (
A.①②③
B.①②④
C.①③④
D.②③④
①函数$ f(x) $的最小正周期为$\pi$;
②函数$ f(x) $的图象经过点$\left(0, \frac{3}{2}\right)$;
③函数$ f(x) $的图象关于点$\left(\frac{5\pi}{12}, 1\right)$对称;
④函数$ f(x) $的图象关于直线$ x = -\frac{\pi}{6} $对称.
则这3个条件的序号可以是 (
AB
)A.①②③
B.①②④
C.①③④
D.②③④
答案:
6.AB解析:若①正确,则$\frac {2\pi}{\omega} = \pi$,解得$\omega = 2$;若②正确,则$f(0) = \cos \varphi + 1 = \frac {3}{2}$,$\cos \varphi = \frac {1}{2}$,$|\varphi| < \pi$,故$\varphi = \pm \frac {\pi}{3}$;若③正确,则$\frac {5\pi\omega}{12} + \varphi = \frac {\pi}{2} + k_1\pi$,$k_1 \in \mathbf {Z}$;若④正确,则$- \frac {\pi\omega}{6} + \varphi = k_2\pi$,$k_2 \in \mathbf {Z}$;对选项A:$\omega = 2$,取$\varphi = - \frac {\pi}{3}$,$\frac {5\pi}{6} - \frac {\pi}{3} = \frac {\pi}{2}$,满足条件,此时④不满足,正确;对选项B:$\omega = 2$,取$\varphi = \frac {\pi}{3}$,$-\frac {\pi}{3} + \frac {\pi}{3} = 0$,满足条件,此时③不满足,正确;对选项C:$\frac {5\pi}{12} + \frac {\pi}{6} = \frac {7\pi}{12} = \left( \frac {1}{4} + \frac {k}{2} \right) T = \left( \frac {1}{4} + \frac {k}{2} \right) \pi$,$k \in \mathbf {N}$,$k = \frac {2}{3}$,不成立,错误;对选项D:相减得到$\frac {5\pi}{12}\omega + \frac {\pi}{6} - (-\frac {\pi}{6}\omega + \varphi) = \frac {\pi}{2} + k_3\pi$,$k_3 \in \mathbf {Z}$,则$\omega = \frac {12}{7} \left( \frac {1}{2} + k_3 \right)$,$k_3 \in \mathbf {Z}$,此时$-\frac {\pi}{6}\omega + \varphi = - \frac {\pi}{6} × \frac {12}{7} \left( \frac {1}{2} + k_3 \right) + \varphi = \frac {-2}{7} \left( \frac {1}{2} + k_3 \right) \pi + \varphi = k_2\pi$,整理得$7\varphi = (7k_2 + 2k_3) \pi + \pi$,$k_2$,$k_3 \in \mathbf {Z}$,而$\varphi = \pm \frac {\pi}{3}$,故不成立,错误。故选AB。
7. * 若$ f(x) = 2\sin\left(2x + \frac{\pi}{6}\right) - 1 $,且$ f(x_1) · f(x_2) = -3 $,则$|x_1 - x_2|$的最小值为 (
A.$\pi$
B.$\frac{\pi}{2}$
C.$2\pi$
D.$\frac{\pi}{4}$
B
)A.$\pi$
B.$\frac{\pi}{2}$
C.$2\pi$
D.$\frac{\pi}{4}$
答案:
7.B解析:$f(x) = 2 \sin \left( 2x + \frac {\pi}{6} \right) - 1$周期为$T = \pi$,值域为$[-3,1]$,即$f(x)_{\max} = 1$,$f(x)_{\min} = -3$,则$\begin{cases}-3 \leqslant f(x_1) \leqslant 1 \\-3 \leqslant f(x_2) \leqslant 1 \\-3 \leqslant f(x_1)f(x_2) \leqslant 9\end{cases}$,由$f(x_1)f(x_2) = -3$,得$\begin{cases}f(x_1) = 1 \\f(x_2) = -3\end{cases}$或$\begin{cases}f(x_2) = 1 \\f(x_1) = -3\end{cases}$,即$f(x_1)$,$f(x_2)$为函数的最大值与最小值,或最小值与最大值,当$x_1$,$x_2$对应$f(x)$图象上相邻两最值点时,$|x_1 - x_2|$的值最小,故$|x_1 - x_2|_{\min} = \frac {T}{2} = \frac {\pi}{2}$。故选B。
查看更多完整答案,请扫码查看


