《2025年经纶学典学霸黑白题高中数学必修第一册苏教版》

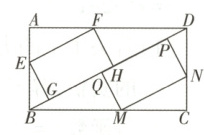
9. $\boldsymbol{\bigstar\bigstar\bigstar}$ (2025·河北石家庄高一月考)如图,某蛋糕店制作一块长为$8\sqrt{5}\ cm$,宽为$4\sqrt{5}\ cm$的矩形双拼水果蛋糕$ABCD$,点$E$,$F$,$M$,$N$分别在线段$AB$,$AD$,$BC$,$CD$上(不包含端点),点$G$,$Q$,$H$,$P$均在线段$BD$上,要在矩形$EFHG$与矩形$MNPQ$两个区域中分别铺满蓝莓与芒果两种水果.设$BG = DP = x\ cm$,铺满水果的区域面积为$S\ cm^2$.
(1)已知$S = ax^2 + bx$,求常数$a$,$b$的值;
(2)已知蛋糕店内的芒果原料充足,但蓝莓至多能铺满$30\ cm^2$,若要求该蛋糕铺满水果的区域面积不小于$35\ cm^2$,求$EF$的取值范围.

答案： 9.解：
(1)易知矩形$EFGH$与矩形$MNPQ$全等，$\tan \angle ABD = \frac{EG}{BG} = \frac{AD}{AB} = 2$，所以$EG = 2BG = 2x$ cm，$\tan \angle ADB = \frac{AB}{AD} = \frac{FH}{DH} = \frac{1}{2}$，所以$DH = 2FH = 2EG = 4x$ cm。又因为$BD = \sqrt{AB^2 + AD^2} = \sqrt{(4\sqrt{5})^2 + (8\sqrt{5})^2} = 20$（cm），所以$GH = BD - BG - DH = 20 - x - 4x = (20 - 5x)$ cm，所以$S = 2EG · GH = 4x(20 - 5x) = -20x^2 + 80x$，又因为$S = ax^2 + bx$，则$a = -20$，$b = 80$。
(2)由
(1)可知，$\begin{cases} x ＞ 0, \\ 20 - 5x ＞ 0, \end{cases}$解得$0 ＜ x ＜ 4$，因为蓝莓至多能铺满$30$ cm²，若要求该蛋糕铺满水果的区域面积不小于$35$ cm²，则$\begin{cases} -10x^2 + 40x \leq 30, \\ x^2 - 4x + 3 \geq 0, \\ 0 ＜ x ＜ 4, \end{cases}$整理可得$\begin{cases} -20x^2 + 80x \geq 35, \\ 0 ＜ x ＜ 4, \\ \frac{1}{2} \leq x \leq 1 或 3 \leq x \leq \frac{7}{2}. \end{cases}$因为$EF = GH = 20 - 5x$，当$\frac{1}{2} \leq x \leq 1$时，$15 \leq 20 - 5x \leq \frac{35}{2}$；当$3 \leq x \leq \frac{7}{2}$时，$\frac{5}{2} \leq 20 - 5x \leq 5$。所以$\frac{5}{2} \leq EF \leq 5$或$15 \leq EF \leq \frac{35}{2}$（单位：cm）。

10. $\boldsymbol{\bigstar\bigstar}$ (2025·江苏无锡高一月考)已知函数$y = (m + 1)x^2 - (m - 1)x + m - 1$.
(1)若不等式$y ＜ 0$的解集为$\mathbf{R}$,求$m$的取值范围;
(2)解关于$x$的不等式$y \geq (1 - m)x$;
(3)若不等式$y \geq m(x^2 + 2) - 3$对一切$x \in \left[-\dfrac{1}{2}, \dfrac{1}{2}\right]$恒成立,求$m$的取值范围.

答案：
10.解：
(1)由已知$(m + 1)x^2 - (m - 1)x + m - 1 ＜ 0$的解集为$\mathbf{R}$，当$m + 1 = 0$，即$m = -1$时，不等式为$2x - 2 ＜ 0$，解集为$x ＜ 1$，不成立；当$m + 1 \neq 0$时，$\begin{cases} m + 1 ＜ 0, \\ \Delta = [-(m - 1)]^2 - 4(m + 1)(m - 1) ＜ 0, \end{cases}$解得$m ＜ -\frac{5}{3}$。综上所述，$m$的取值范围为$(-\infty, -\frac{5}{3})$。
(2)不等式$y \geq (1 - m)x$，即$(m + 1)x^2 - (m - 1)x + m - 1 \geq (1 - m)x$，即$(m + 1)x^2 + m - 1 \geq 0$，当$m + 1 = 0$，即$m = -1$时，不等式为$-2 \geq 0$不成立，解集为$\varnothing$；当$m + 1 \neq 0$时，不等式对应方程为$(m + 1)x^2 + m - 1 = 0$，$\Delta = -4(m + 1)(m - 1)$，当$m ＜ -1$时，$\Delta ＜ 0$，不等式解集为$\varnothing$；当$-1 ＜ m ＜ 1$时，不等式解集为$(-\infty, -\sqrt{\frac{1 - m}{1 + m}}) \cup (\sqrt{\frac{1 - m}{1 + m}}, +\infty)$；当$m \geq 1$时，不等式的解集为$\mathbf{R}$。
(3)方法一：不等式$y \geq m(x^2 + 2) - 3$，对$x \in [-\frac{1}{2}, \frac{1}{2}]$恒成立可转化为$x^2 + (1 - m)x + 2 - m \geq 0$，对$x \in [-\frac{1}{2}, \frac{1}{2}]$恒成立，记二次函数$w = x^2 + (1 - m)x + 2 - m$，开口向上，对称轴为直线$x = \frac{1 - m}{2}$，满足函数在$x \in [-\frac{1}{2}, \frac{1}{2}]$时图象恒在$x$轴上方，画出示意图如下，有三种可能性：
　　 　
由图可得$\begin{cases} \frac{1 - m}{2} \leq -\frac{1}{2}, \\ (-\frac{1}{2})^2 + (1 - m) · (-\frac{1}{2}) + 2 - m \geq 0 \end{cases}$或$\Delta = (1 - m)^2 - 4(2 - m) \leq 0$或$\begin{cases} \frac{1 - m}{2} \geq \frac{1}{2}, \\ (\frac{1}{2})^2 + (1 - m) · \frac{1}{2} + 2 - m \geq 0, \end{cases}$解得$m \leq 2\sqrt{2} - 1$，即$m \in (-\infty, 2\sqrt{2} - 1]$。
方法二：不等式$y \geq m(x^2 + 2) - 3$，对$x \in \{x \mid -\frac{1}{2} \leq x \leq \frac{1}{2}\}$恒成立可转化为$m(x + 1) \leq x^2 + x + 2$，对$x \in [-\frac{1}{2}, \frac{1}{2}]$恒成立，所以$x + 1 \in [\frac{1}{2}, \frac{3}{2}]$，则$m \leq \frac{x^2 + x + 2}{x + 1} = x + 1 + \frac{1}{x + 1}$，设$z = x + 1 + \frac{1}{x + 1} \geq 2\sqrt{2} - 1$，当且仅当$x + 1 = \frac{1}{x + 1}$，即$x = \sqrt{2} - 1$时，等号成立，所以$m \leq 2\sqrt{2} - 1$，即$m \in (-\infty, 2\sqrt{2} - 1]$。

$\boldsymbol{\bigstar\bigstar\bigstar}$ (2025·江苏常州高级中学高一月考)若关于$x$的不等式$0 \leq ax^2 + bx + c \leq 2(a ＞ 0)$的解集为$[-1, 3]$,则$a - b - c$的取值范围是(-2, 1].

答案： 压轴挑战
$(-2, 1]$ 解析：因为不等式$0 \leq ax^2 + bx + c \leq 2 (a ＞ 0)$的解集为$[-1, 3]$，所以二次函数$y = ax^2 + bx + c$的对称轴为直线$x = 1$，且需满足$\begin{cases} a - b + c = 2, \\ 9a + 3b + c = 2, \\ a + b + c \geq 0, \\ 3a + 2 \geq 0, \end{cases}$解得$\begin{cases} b = -2a, \\ c = -3a + 2, \end{cases}$所以$a + b + c = a - 2a - 3a + 2 \geq 0$，$3a + 2 \geq 0 \Rightarrow a \leq \frac{1}{2}$，所以$a \in (0, \frac{1}{2}]$，所以$a - b - c = a + 2a + 3a - 2 = 6a - 2 \in (-2, 1]$。故答案为$(-2, 1]$。