《2025年经纶学典学霸黑白题高中数学必修第一册苏教版》

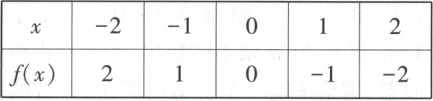
1. 设已知函数$ f(x) $如下表所示:则不等式$ f(f(x)) \geq 0 $的解集为(A)


A.$ \{ 1,2,0 \} $
B.$ \{ -1,-2,0 \} $
C.$ \{ 1,2 \} $
D.$ \{ -1,-2 \} $

答案： 1.A 解析：由f(f(x))≥0,得f(x)=0或f(x)=-1或f(x)=-2,当f(x)=0时,x=0,当f(x)=-1时,x=1,当f(x)=-2时,x=2,综上所述,不等式f(f(x))≥0的解集为{1,2,0}.故选A.

2. 若$ f(x) $是一次函数,$ 2f(2) - 3f(1) = 5 $,$ 2f(0) - f(-1) = 1 $,则$ f(x) = $(B)

A.$ 3x + 2 $
B.$ 3x - 2 $
C.$ 2x + 3 $
D.$ 2x - 3 $

答案： 2.B 解析：设f(x)=ax+b(a≠0),由题设有$\begin{cases}2(2a+b)-3(a+b)=5,\\2(0·a+b)-(-a+b)=1,\end{cases}$解得$\begin{cases}a=3,\\b=-2,\end{cases}$所以f(x)=3x-2.故选B.

3. * (2025·江苏南京师大附中高一期中)设函数$ f(x) = \begin{cases}f(x + 2), & x \leq 0, \\ x^2 - 3x, & x ＞ 0,\end{cases}$则$ f(-4) = $( )

A.$ -4 $
B.$ -2 $
C.$ 0 $
D.$ 2 $

答案： 3.B 解析：f(-4)=f(-2)=f
(0)=f
(2)=$2^2-3×2=-2$.故选B.

4. * (2025·山东济宁高一期中)某市一天内的气温$ Q(t) $(单位:$ ° C $)与时刻$ t $(单位:时)之间的关系如图所示,令$ C(t) $表示时间段$ [0,t] $内的温差(即时间段$ [0,t] $内最高温度与最低温度的差),$ C(t) $与$ t $之间的函数关系用下列图象表示,则下列图象最接近的是(D)

答案： 4.D 解析：由题意C(t)从0到4逐渐增大,从4到8不变,从8到12逐渐增大,从12到20不变,从20到24又逐渐增大,从4到8不变,是常数,该常数为2,只有D满足.故选D.

5. * (多选)(2025·吉林白城高一期中)已知函数$ y = f(x) $的图象由如图所示的两段线段组成,则(BD)


A.$ f(f(3)) = 1 $
B.不等式$ f(x) \leq 1 $的解集为$ \left[ 2, \frac{10}{3} \right] $
C.函数$ f(x) $在区间$ [2,3] $上的最大值为$ 2 $
D.$ f(x) $的解析式可表示为$ f(x) = x - 3 + 2|x - 3|(x \in [0,4]) $

答案： 5.BD 解析：根据题意可得,在区间[0,3]上,函数图象为线段,经过点(0,3)和(3,0),则其解析式为f(x)=3-x(0≤x≤3),在区间[3,4]上,函数图象为线段,经过点(3,0)和(4,3),设f(x)=kx+b,x∈[3,4],则$\begin{cases}3k+b=0,\\4k+b=3,\end{cases}$解得$\begin{cases}k=3,\\b=-9,\end{cases}$所以其解析式为f(x)=3x-9(3≤x≤4),
综合可得f(x)=$\begin{cases}3-x,0\leq x\leq3,\\3(x-3),3＜x\leq4,\end{cases}$
对于A,f
(3)=0,则f(f
(3))=f
(0)=3,故A错误;对于B,若f(x)≤1,则有$\begin{cases}3-x\leq1,\\0\leq x\leq3,\end{cases}$或$\begin{cases}3(x-3)\leq1,\\3＜x\leq4,\end{cases}$解得2≤x≤3或3＜x≤$\frac{10}{3}$,即不等式的解集为$[2,\frac{10}{3}]$,故B正确;对于C,在区间[2,3]上,f(x)=3-x的值逐渐减小,其最大值为f
(2)=1,故C错误;对于D,由f(x)=x-3+2|x-3|(x∈[0,4])=$\begin{cases}3-x,0\leq x\leq3,\\3(x-3),3＜x\leq4,\end{cases}$故D正确.故选BD.

6. * (2025·广州肇庆高一期中)已知$ f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2} $,则函数$ f(x) = $ $x^2-2(|x|\geq2)$.

答案： 6.$x^2-2(|x|\geq2)$ 解析：f($x+\frac{1}{x}$)=$x^2+\frac{1}{x^2}=(x^2+2+\frac{1}{x^2})-2=(x+\frac{1}{x})^2-2$,所以f(x)=$x^2-2(|x|\geq2)$.

7. * (2025·山东济南高一月考)某种物资实行阶梯价格制度:年用量不超过10千克的部分价格为6元/千克;超过10千克而不超过20千克的部分价格为8元/千克;超过20千克的部分价格为10元/千克.则一户居民使用该物资的年花费$ y $(元)关于年用量$ x $(千克)的函数解析式为 .若某户居民使用该物资的年花费为100元,则该户居民的年用量为 千克.

答案： 7.y=$\begin{cases}6x,x\in(0,10],\\8x-20,x\in(10,20],\\10x-60,x\in(20,+\infty)\end{cases}$ 15 解析：由题可得,当0＜x≤10时,y=6x,当10＜x≤20时,y=6×10+8(x-10)=8x-20,当x＞20时,y=6×10+8×10+10(x-20)=10x-60,
∴y=$\begin{cases}6x,x\in(0,10],\\8x-20,x\in(10,20],\\10x-60,x\in(20,+\infty)\end{cases}$ 若某户居民使用该物资的年花费为100元,可得该户居民的年用量在(10,20]内,则8x-20=100,解得x=15,则该户居民的年用量为15千克.故答案为y=$\begin{cases}6x,x\in(0,10],\\8x-20,x\in(10,20],\\10x-60,x\in(20,+\infty)\end{cases}$ 15;

8. 设集合$ A = \left[ 0, \frac{1}{2} \right) $,$ B = \left[ \frac{1}{2}, 1 \right] $,函数$ f(x) = \begin{cases}x + \frac{1}{2}, & x \in A, \\ 2 - 2x, & x \in B,\end{cases}$已知实数$ x_0 \in A $,且$ f(f(f(x_0))) \in A $,则$ x_0 $的取值范围为 ______ .

答案： 8.($\frac{1}{4}$,$\frac{1}{2}$) 解析：依题意,f(x)=$\begin{cases}x+\frac{1}{2},x\in[0,\frac{1}{2}),\\2-2x,x\in[\frac{1}{2},1],\end{cases}$ $x_0\in A$,即$x_0\in[0,\frac{1}{2})$,所以f($x_0$)=$x_0+\frac{1}{2}\in[\frac{1}{2},1)$,所以f(f($x_0$))=f($x_0+\frac{1}{2}$)=2-2($x_0+\frac{1}{2}$)=1-2$x_0$,依题意1-2$x_0\in[0,\frac{1}{2})$,-2$x_0\in[-1,-\frac{1}{2})$,$x_0\in(\frac{1}{4},\frac{1}{2}]$,而$x_0\in[0,\frac{1}{2})$,所以$x_0$的取值范围为($\frac{1}{4}$,$\frac{1}{2}$).故答案为($\frac{1}{4}$,$\frac{1}{2}$).

* (2025·广东广州高一期中)已知函数$ f(x) $的定义域为$ \mathbf{R} $,且$ f(x + y) - 2f(x - y) + f(x) - 2f(y) = y - 2 $,则$ f(2\ 024) = $(D)

A.$ 0 $
B.$ 1 $
C.$ 2\ 024 $
D.$ 2\ 025 $

答案： D 解析：令x=y=0可得-2f
(0)=-2,所以f
(0)=1,再令x=0可得f(y)-2f(-y)+f
(0)-2f(y)=y-3,即-f(y)-2f(-y)=y-3②,将上式中的y全部换成-y可得-f(-y)-2f(y)=-y-3②,联立①②可得f(y)=y+1,所以f
(2024)=2024+1=2025.故选D.